Inhaltsverzeichnis 1 Einführung in die Modellkalibrierung 1.1 Motivation 1.2 Vorbereitung der Kalibrierung 1.2.1 Datenprüfung 1.2.2 Auswahl der zu kalibrierenden Parameter und Definition des Parameterraums 1.2.3 Spezifikation von Gütekriterien und Zielfunktionen 1.3 Identifikation von Modellparametern 1.3.1 Äquifinalität 1.4 Modellvalidierung 1.4.1 Split Sample Validierung 1.4.2 Kreuzvalidierung 1.4.3 Proxy Basin Test 1.4.4 Differential Split-Sample Test 1.4.5 Proxy-basin Differential Split-Sample Test 2 Voraussetzung für die Modellkalibrierung mit JAMS 3 Modellkalibrierung mit JAMS 3.1 Offline Kalibrierung 3.2 Online Kalibrierung (nur für JAMS-2 Modelle) 3.3 OPTAS Bedienung

Einführung in die Modellkalibrierung

Motivation

Die Modellierung hydrologischer Prozesse ist aufgrund zahlreicher Faktoren eine herausfordernde Aufgabe: Das Untersuchungsgebiet kann sich sowohl zeitlich als auch räumlich über große Skalen erstrecken. Hydrologische Prozesse finden kontinuierlich auf vielen verschiedenen Skalen statt und hängen von vielen verschiedenen Systemvariablen ab, die durch komplexe nicht-lineare Beziehungen interagieren (Blöschl und Sivapalan, 1995). Für die meisten Fragestellungen ist die Untersuchung eines einzigen unabhängigen Prozesses des hydrologischen Systems nicht ausreichend. Vielmehr ist ein umfassendes Verständnis der Interaktionen der vielfältigen Systemkomponenten und -prozesse erforderlich, welches Wissen aus den unterschiedlichsten Disziplinen erfordert.

Erschwerend kommt hinzu, dass viele dieser Prozesse unterhalb der Erdoberfläche ablaufen und daher schwer messbar sind. Weiterhin lassen sich die hydrologischen Systemgrößen nicht in ihrer Gesamtheit beobachten, da Messwerte nie kontinuierlich vorliegen, sondern stets diskret ermittelt werden müssen.

Dies ist insbesondere für Systemzustände problematisch, die räumlich und zeitlich stark variabel sind, so dass repräsentative Messungen sehr aufwändig sind (Wainwright und Mulligan, 2004).

Aus diesem Grund sind die Komponenten aller hydrologischen Modelle zu einem gewissen Grad konzeptionelle Beschreibungen der realen Prozesse (Crawford und Linsley, 1966). Obwohl diese Tatsache bereits vor 45 Jahren zutraf, ist sie auch heute noch gültig und eine baldige Änderung ist nicht zu erwarten (Duan et al., 2003). Als Konsequenz ergibt sich, dass die Modellparameter in vielen Fällen nicht direkt bestimmt werden können, da sie keinen direkten physikalischen Zusammenhang aufweisen oder Messungen praktisch nicht durchführbar sind (Gupta et al., 2005). Deshalb werden die Parameter indirekt bestimmt, indem nach einer Modellparametrisierung gesucht wird, die zur bestmöglichen Anpassung der Simulation an das natürliche System führt. Für eine erfolgreiche Anwendung der Modelle ist eine sorgfältige Bestimmung der Modellparameter essenziell. Meist stehen die Modellausgaben in nichtlinearer Beziehung zu den Modellparametern und die zugrunde liegenden Modelle sind analytisch nicht behandelbar. Deshalb können meist keine direkten Lösungsverfahren angewendet werden, so dass die Parameter in einem „trial-and-error“ Prozess bestimmt werden müssen (Gupta et al., 2005).

Eine Sonderrolle im Kalibrierungsprozess nehmen unbemessene Flusseinzugsgebiete oder Gebiete mit sehr schlechter Datenlage ein, da in diesem Fall die Kalibrierung nicht direkt erfolgen kann. Zur Überwindung des Problems werden Modelle mit starker physikalischen Basis (Koren et al., 2003) verwendet, statistische Analysen durchgeführt (z. B. Jakeman et al. 1992; Wagener et al. 2004) oder Mischformen aus beiden eingesetzt. Für stark physikalisch-basierte Modelle können viele Parameter, entweder direkt oder durch empirische Gleichungen aus den Eigenschaften des Gebiets abgeleitet werden. Die statistische Analyse stellt im Unterschied dazu eine statistische Beziehung zwischen den Parameterwerten und Gebietseigenschaften her. Modelle unbemessener FEG werden in dieser Arbeit nicht betrachtet, so dass nun die Kalibrierung an beobachteten Systemzuständen geschildert wird.

Vorbereitung der Kalibrierung

Im Vorfeld der Kalibrierung sind mehrere Entscheidungen notwendig, die in Abhängigkeit des Modellzwecks getroffen werden müssen. Dazu gehören nach Grundmann (2009):

1. Auswahl der Daten, an denen die Kalibrierung des Modells erfolgt
2. Auswahl der zu kalibrierenden Parameter und Definition des Parameterraums
3. Spezifikation von Gütekriterien und Zielfunktionen
4. Auswahl einer Optimierungsstrategie
5. Auswahl einer Strategie zur Validierung und Unsicherheitsanalyse

Datenprüfung

Für eine erfolgreiche Kalibrierung ist eine sorgfältige Prüfung der Daten hinsichtlich Konsistenz und Homogenität eine wichtige Voraussetzung (Grundmann, 2009). Die Kalibrierung kann an sehr unterschiedlichen Beobachtungen erfolgen. Es existieren zahlreiche Arbeiten die Messungen des Grundwasserstandes (Blazkova et al., 2002; Madsen, 2003), der Schneebedeckung (Bales und Dozier, 1998), der Bodenfeuchte (Merz und Bárdossy, 1998; Western und Grayson, 2000; Scheffler, 2008) und Evapotranspiration (Immerzeel und Droogers, 2008) verwenden. Jedoch werden hydrologische Modelle in den meisten Fällen an gemessenen Abflussganglinien kalibriert (Seibert, 2000). Die Gründe hierfür sind, dass (i) für viele Gewässer eine langjährige Abflusszeitreihe vorhanden ist, (ii) der Abfluss ein aggregiertes Signal fast aller hydrologisch relevanten Prozesse des gesamten Flusseinzugsgebiets darstellt, welches (iii) relativ geringen Messfehlern unterliegt und (iv) zeitlich oft hoch aufgelöst ist. Aus diesen Gründen wird die Kalibrierung oft anhand der Abflussganglinie durchgeführt.

Auswahl der zu kalibrierenden Parameter und Definition des Parameterraums

Die Frage nach der Auswahl der zu kalibrierenden Parameter ist meist nicht trivial. Sie hängt von dem zu kalibrierenden Modell und dessen Anwendung ab. Viele hydrologische Modelle besitzen mehr Parameter als kalibriert werden können. Es sollten daher nur diejenigen Parameter kalibriert werden, die sich nicht direkt ableiten lassen (z. B. aus den Landschaftsmerkmalen) und die signifikanten Einfluss auf das Modellverhalten haben. Die Identifikation dieser Parameter kann durch eine Sensitivitätsanalyse des Modells bewältigt werden. Diese gibt aber nicht nur Aufschluss über die quantitative Wirkung der Parameter, sondern leistet auch einen erheblichen Beitrag zum Modellverständnis (Saltelli et al., 2008).

Auch die Definition der Parametergrenzen ist meistens nicht offensichtlich. Je nach Grad des physikalischen Zusammenhangs können Grenzwerte und geeignete Standardwerte der Parameter (i) direkt durch Messungen (entweder unter Laborbedingungen oder im realen System) bestimmt werden, (ii) aus Plausibilitätsbetrachtungen abgeleitet werden oder (iii) aus Erfahrungs- und Literaturwerten übertragen werden. Weiterhin stellen viele Modelldokumentationen Empfehlungen zur Wahl der Parametergrenzen bereit (siehe z. B. DYRESM (Hamilton und Schladow, 1997), J2000 (Krause, 2001), WaSim-ETH (Schulla und Jasper, 2000)). Diese Grenzen sind meist sehr weit gefasst, da sie die initiale Unsicherheit der Parameter bei fehlendem Wissen über die Modellanwendung reflektieren.
Eine Einführung in die Kalibrierungsparameter der Modelle J2000 und J2000g ist hier und hier zu finden

Spezifikation von Gütekriterien und Zielfunktionen

Die Aufgabe der Kalibrierung ist es, die Parameterunsicherheit schrittweise auf ein Minimum zu reduzieren. Für diese Optimierung ist die vergleichende Bewertung der simulierten Hydrographen erforderlich. Obwohl die visuelle Begutachtung des Hydrographen durch einen Experten die wichtigste Methode ist, um die Leistung des Modells zu beurteilen (Krause et al., 2005), wird für die objektive quantifizierbare Bewertung eine mathematische Fehlerfunktion benötigt. Fehlerfunktionen repräsentieren den Anteil der gemessenen Daten, der nicht durch das Modell reproduziert wird. Prinzipiell lassen sich absolute und relative Fehlerfunktionen unterscheiden. Relative Fehlerfunktionen besitzen den Vorteil der Dimensionslosigkeit, d. h. sie können anwendungsübergreifend verglichen werden. Fehlerfunktionen, die im hydrologischen Kontext sehr häufig eingesetzt werden, sind u. a. die Nash-Sutcliffe Effizienz (Nash und Sutcliffe, 1970) und deren Modifikationen, das Bestimmtheitsmaß und der absolute bzw. relative Volumenfehler (Krause et al., 2005).

Krause et al. (2005) kommen durch den Vergleich mehrerer Fehlerfunktionen zu dem Schluss, dass keines der Maße alle relevanten Aspekte eines Hydrographen gleichermaßen berücksichtigt und jedes Maß spezifische Vor- und Nachteile aufweist. Obwohl in den letzten Jahren zahlreiche neue Fehlerfunktionen vorgeschlagen wurden, um diesen Defiziten entgegenzuwirken, konnte die Frage nach einem universell geeigneten Maß bisher nicht beantwortet werden. Ein Übersicht verschiedener Fehlermaße und deren Charakterisitik ist hier dargestellt.

Identifikation von Modellparametern

Die Suche nach geeigneten Parametersätzen kann entweder manuell oder automatisch durchgeführt werden. Der manuelle Ansatz kann zu hervorragenden Resultaten führen, ist jedoch mühsam, mit hohem personellen Zeitaufwand und Kosten verbunden und unterliegt subjektiven Entscheidungsprozessen (Boyle et al., 2000). Eine Alternative hierzu bietet die automatische Kalibrierung mit mathematischen Optimierungsverfahren, die schnell und objektiv komplexe Probleme bewältigen können.

In der Vergangenheit wurde die automatische Kalibrierung mit lokalen Optimierungsverfahren, wie dem Gradientenabstieg durchgeführt. Es wurde jedoch schnell offensichtlich, dass sich mit diesem Ansatz optimale Parametersätze nicht zuverlässig auffinden lassen, da das Optimierungsproblem zahlreiche ungünstige Eigenschaften aufweist (Duan et al., 1992). Daher entwickelten Duan et al. (1992) das Shuffled Complex Evolution (SCE) Verfahren, welches sich in den letzten 20 Jahren als robustes, effizientes und effektives Verfahren bewährt hat und bis heute häufig im hydrologischen Umfeld verwendet wird (z. B. Sorooshian et al. 1993, Eckhardt und Arnold 2001, Liong und Atiquzzaman 2004).

Generell sollte die Kalibrierung aber nicht nur als Suche nach einem Parametersatz verstanden werden, der zur besten Angleichung des Modells an die Datenlage führt (Vidal et al., 2007), sondern vielmehr als fortschreitender Prozess der Parameteridentifikation. Dabei wird die initiale Unsicherheit nach und nach reduziert, indem der Parameterraum auf diejenigen Parametersätze eingeschränkt wird, die zu einem Modellverhalten führen, welches mit dem beobachteten Systemverhalten qualitativ und quantitativ konsistent ist. Hierbei darf nicht erwartet werden, dass eine exakte Übereinstimmung des Modells mit der Realität erreicht werden kann. Denn jede Modellstruktur und -parametrisierung ist bestenfalls eine Approximation der wahren Systemstruktur und jede Modellprognose ist mit einer gewissen Unsicherheit behaftet. Gupta et al. (2005) charakterisieren ein kalibriertes hydrologisches Modell folgendermaßen:

1. Das Ein-/Ausgabeverhalten des Modells ist konsistent mit dem beobachteten Einzugsgebietsverhalten.
2. Die Modellvorhersagen sind akkurat (d. h. sie haben einen vernachlässigbar kleinen systematischen Fehler) und präzise (d. h. die Unsicherheit der Prognosen ist gering) und robust. Dies bedeutet, dass kleine Änderungen der Parameter auch nur zu kleinen Änderungen im Modellergebnis führen.
3. Die Modellstruktur und das Modellverhalten sind konsistent mit dem gegenwärtigen hydrologischen Verständnis des realen Systems.

Äquifinalität

Die Identifikation von Modellparametern aus einem Impuls-/Antwortverhalten ist unter dem Begriff inverses Problem oder Identifizierbarkeitsproblem (Cobelli und DiStefano III., 1980) bekannt und tritt nicht nur im hydrologischen Kontext auf. Inverse Probleme sind oft schlecht gestellt (Kabanikhin, 2008), das heißt sie besitzen entweder keine Lösung, unendlich viele Lösungen oder das System verhält sich chaotisch. Bellman und Astrom (1970) konnten formal zeigen, dass das Inverse Problem bereits für relativ einfache Systeme nicht eindeutig lösbar ist, sofern nicht alle internen Zustände des Systems beobachtbar sind. Für die hydrologische Modellierung bedeutet dies, dass das Systemverhalten meistens durch verschiedene Modelle mit unterschiedlichen Strukturen und Parametrisierungen erklärt werden kann. Für dieses Phänomen hat Beven (1993) den Begriff Äquifinalität geprägt, der ursprünglich auf Ludwig von Bertalanffy zurückgeht (Von Bertalanffy et al., 1950). Äquifinalität ist ein Ausdruck dessen, dass die verfügbaren Informationen nicht ausreichen, um ein System vollständig zu beschreiben. Nach Wagener und Gupta (2005) existieren drei Philosophien zum Umgang mit diesem Phänomen:

• Parsimonie: Äquifinalität oder Parameterunsicherheit kann als Hinweis dafür aufgefasst werden, dass die gewählte Modellstruktur in Anbetracht der Datenlage zu komplex ist. Ausgangspunkt dieser Philosophie ist die Beobachtung, dass einfache, weniger datenintensive Modelle oft gute und bessere Prognosen liefern als komplexe physikalisch basierte Modelle (Loague und Freeze, 1985; Reed et al., 2004). Das Prinzip der Parsimonie besagt, dass stets die einfachste mögliche Erklärung für ein Phänomen verwendet werden sollte. Dieses Prinzip wurde bereits durch Aristoteles vertreten und durch William of Occam zu Beginn des 14. Jahrhunderts postuliert, so dass oft der Begriff „Occam´s Razor“ verwendet wird. Dieser Regel folgend sollte die Struktur hydrologischer Modelle so einfach wie möglich sein und nur dann Komplexität hinzugefügt werden, wenn die Präzision des Modells für den intendierten Zweck nicht ausreichend ist. Mehrere Arbeiten zeigen, dass die Parameterunsicherheit durch die Verringerung der Modellkomplexität reduziert werden kann (Jakeman und Hornberger, 1993; Wheater und Jakeman, 1993; Young et al., 1996; Wagener et al., 2002, 2003b).

• Effiziente Informationsnutzung: Traditionell wird für die Kalibrierung ein einzelnes Zielkriterium verwendet. Durch diese einkriterielle Optimierung wird die Ähnlichkeit zwischen dem simulierten und beobachteten Abfluss auf einen einzigen numerischen Wert reduziert, obwohl die Ausgangsdaten meist aus tausenden Datensätzen bestehen. Dieser Informationsverlust ist nach Gupta et al. (1998) ein Grund für das Auftreten der Äquifinalität. Es gibt zwei Ansätze, um diesem Informationsverlust entgegenzuwirken: Erstens argumentieren Gupta et al. (1998), dass die Suche nach optimalen Parametersätzen an sich ein multikriterielles Problem ist. Die multikriterielle Optimierung berücksichtigt bei der Kalibrierung mehrere Zielkriterien gleichzeitig. Dadurch wird die Informationsmenge vervielfacht und der Äquifinalität entgegengewirkt, so dass dieser Ansatz im letzten Jahrzehnt verstärkt Einzug gehalten hat. Der zweite Ansatz besteht darin, die in den Daten enthaltene Information durch Unterteilung der Datenmenge besser zu extrahieren. Methoden, die hierfür angewendet werden können, sind der Kalman Filter und seine Erweiterungen (Kitanidis und Bras, 1980), PIMLI (Vrugt et al., 2002), BARE (Thiemann et al., 2001) und DYNIA (Wagener et al., 2003a).

• Akzeptanz der Äquifinalität: Äquifinalität kann auch als inhärente Eigenschaft des Problems aufgefasst werden. Die logische Konsequenz besteht darin alle potentiellen Lösungen des Kalibrierungsproblems beizubehalten und in die Modellierung einzubeziehen, sofern diese nicht aus anderen Gründen ausgeschlossen werden können. Dieses Ensemble aus Lösungen kann beispielsweise für die Analyse der Parameterunsicherheit mit der Generalized Likelihood Uncertainty Estimation Methode (GLUE, Beven und Freer 2001) oder DREAM (Vrugt et al., 2008) verwendet werden.

Die Handhabung der Äquifinalität ist eng mit der Berücksichtigung von Modellunsicherheiten verbunden. Hydrologische Modelle werden oft in kritischen Systemen eingesetzt, wie zum Beispiel zur Vorhersage von Naturkatastrophen, der Prognose von langfristigen Auswirkungen des Klimawandels oder der Entwicklung von Anpassungsstrategien der Wasserinfrastruktur. Daher ist die Abschätzung, Aufbereitung und Kommunikation der Modellunsicherheit und der Grenzen der Modellprognosen aus gesellschaftlicher Sicht von zentraler Bedeutung (Montanari et al., 2009).

Modellvalidierung

Nach der Kalibrierung ist es erforderlich das Modell an Daten zu validieren, die bisher nicht in den Kalibrierungsprozess eingeflossen sind. Die Modellvalidierung ist ein wichtiges Werkzeug der Qualitätssicherung. Sie weist die Eignung eines Modells für einen intendierten Zweck nach (Bratley et al., 1987). Generell gibt es verschiedene Qualitätskriterien, die für die Modellvalidierung eine Rolle spielen.

Die Genauigkeit und Präzision eines Modells beschreibt die Abweichung der simulierten Werte von realen Messwerten. Die Genauigkeit des Modells kann durch statistische Fehlerfunktionen quantifiziert werden. Da jede Fehlerfunktion spezielle Eigenschaften hat, werden in dieser Arbeit mehrere Fehlerfunktionen verwendet.

Die Korrektheit des Modells bezeichnet die Eigenschaft, korrekte Ergebnisse aus den richtigen Gründen zu berechnen. Dies bedeutet, dass das System durch das Modell korrekt erklärt wird. Eine gute statistische Übereinstimmung der Simulationsergebnisse mit den Messwerten impliziert nicht notwendigerweise eine adäquate Abbildung des hydrologischen Systems (Schaefli und Gupta, 2007). Für die praktische Anwendung ist ein Modell nur dann nützlich, wenn es sich als vertrauenswürdiges Abbild realer Vorgänge erweist (Power, 1993). Dies beinhaltet unter anderem, dass das Verhalten und die Parametrisierung des Modells plausibel sind. Daher ist es wichtig die Simulationsergebnisse einer manuellen Prüfung zu unterziehen.

Ebenso wichtig ist die Abschätzung der Modellunsicherheit. Die Modellunsicherheit hat vielfältige Ursachen. Beispielweise sind die Eingangsdaten des Modells fast immer mit Fehlern und Unsicherheiten behaftet. Weiterhin ist das Wissen über ein natürliches System nie vollständig, so dass die Abbildung der realen Prozesse im Modell Ungewissheiten unterliegt. Darüber hinaus ist die Parametrisierung eines Modells meist nicht eindeutig bestimmbar. Aus der Kombination dieser Unsicherheiten definiert sich der zu erwartende Fehler des Modellergebnisses. Ein Modell wird als robust bezeichnet, wenn sich kleine Änderungen der Eingangsdaten und Modellparameter nur geringfügig auf das Modellergebnis auswirken.

Ein weiteres Qualitätskriterium ist die Generalisierungsfähigkeit. Sie bezeichnet die Fähigkeit des Modells seine Funktion auch bei Änderungen des Systems und der Modellanwendung aufrecht zu erhalten. Ein typisches Beispiel ist die Modellierung unter Veränderungen der Landnutzung in einem Gebiet. Klemeš (1986) gibt hierarchische Stufen zur Prüfung der Generalisierungsfähigkeit an:

Split Sample Validierung

Die verfügbare Menge an Validierungsdaten (z.B. Abflusszeitreihe) wird in zwei Abschnitte geteilt. Zunächst wird der erste Abschnitt für die Kalibrierung des Modells und die zweite für die Validierung verwendet. Anschließend wird die Kalibrierungs- und Validierungsabschnitt getauscht. Daher sollten beide Abschnitte etwa gleich groß sein und eine ausreichend große Datenmenge für eine adäquate Kalibrierung aufweisen. Das Modell kann als akzeptabel eingestuft werden, wenn beide Validierungsresultate ähnlich sind und unter für die Modellanwendung hinreichend gute Eigenschaften aufweisen. Falls die verfügbare Datenmenge nicht ausreichend groß ist für eine 50/50 Teilung, sollte die Teilung derart durchgeführt werden, dass ein Segment für eine sinnvolle Kalibrierung groß genug ist. Der verbleidende Rest wird für die Validierung verwendet. In diesem Fall sollte die Validierung auf zwei verschiedene Weisen durchgeführt werden. Beispielsweise (a) zunächst die ersten 70% der Daten für die Kalibrierung und die verbleibenden 30% für die Validierung (b) anschließend die letzten 70% der Daten für die Kalibrierung und die verbleibenden ersten 30% für die Validierung.

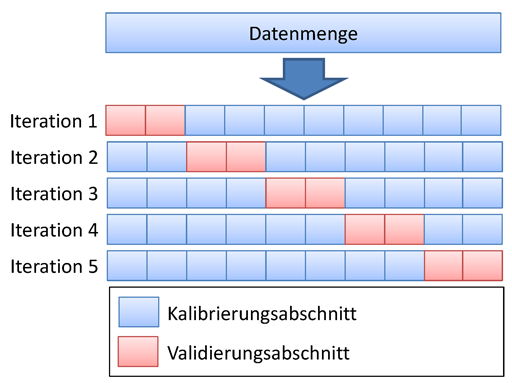
Kreuzvalidierung

Die Kreuzvalidierung ist eine Weiterentwicklung des Split-Sample Tests. Dabei wird die verfügbare Datenmenge in n gleich große Abschnitte aufgeteilt. Nun werden jeweils n − 1 Abschnitte für die Kalibrierung verwendet und der verbleibende Abschnitt für die Validierung. Dabei wird der zu validierende Abschnitt durchgetauscht, so dass jeder Datensatz einmal validiert wurde. Diese Methode ist deutlich rechenaufwändiger als die Split Sample Validierung, hat aber große Vorteile, wenn die Menge der verfügbaren Daten gering ist und bietet die Möglichkeit jeden Datensatz zu validieren. Ein Spezialfall dieser Validierung ist die Leave-One-Out Validierung (LOO). Hierbei wird stets genau ein Datensatz für die Validierung verwendet und die restlichen für die Validierung. Auf Grund des enormen Aufwandes ist diese Art der Validierung meist nur in Spezialfällen möglich.

Proxy Basin Test

Hierbei handelt es sich um einen grundlegenden Test für räumliche Übertragbarkeit eines Modells. Falls beispielsweise der Abfluss in einem nicht bemessenen Gebiet C simuliert werden soll, können zwei bemessene Gebiete A und B innerhalb der Region gewählt werden. Das Modell sollte mit Daten aus Gebiet A kalibriert und mit Daten des Gebiets B validiert werden. Anschließend sollten die Rollen der Gebiete A und B getauscht werden. Nur wenn beide Validierungsergebnisse unter Hinblick der Modellierungsanwendung akzeptabel sind, kann die grundlegende Annahme getroffen werden, dass das Modell in der Lage ist den Abfluss in Gebiet C zu simulieren. Dieser Test sollte auch verwendet werden, wenn ein verfügbarer Datensatz in Gebiet C vorhanden ist, aber für einen Split-Sample Test nicht ausreicht. Der vorhandene Datensatz in Gebiet C würde also nicht für die Modellentwicklung verwendet werden, sondern lediglich als zusätzliche Validierung.

Differential Split-Sample Test

Dieser Test sollte immer dann verwendet werden, wenn ein Modell in einem bemessenen Gebiet unter neuen Bedingungen verwendet werden soll. Dieser Test kann unterschiedliche Varianten aufweisen, abhängig von der Art wie sich Bedingungen/Eigenschaften des Gebietes verändert haben. Hierzu gehören beispielsweise klimatische Veränderungen, Veränderungen in der Landnutzung, Errichtung von Bauwerken, die die Hydrologie im Gebiet beeinflussen und Ähnliches.

Für die Simulation des Effektes durch den Klimawandel, sollte der Test folgende Form haben. Zwei Zeitperioden mit verschiedenen klimatischen Parametern sollten in den historischen Datensätzen identifiziert werden. Beispielsweise eine Zeitperiode mit hohem durchschnittlichen Niederschlägen und eine weitere mit niedrigen Niederschlägen. Falls das Modell für die Abflusssimulation von feuchten Klimaszenarien verwendet werden soll, sollte das Modell mit dem trockenen Datensatz kalibriert werden und mit der Validierung mit dem "feuchten" Datensatz erfolgen. Falls es für die Simulation eines trockenen Szenarios verwendet werden soll, sollte genau umgekehrt vorgegangen werden. Im Allgemeinen sollte die Validierung das Modell unter veränderten Bedingungen testen. Falls in den historischen Daten keine Abschnitte mit signifikant unterschiedlichen klimatischen Parameter identifiziert werden können, sollte das Modell in einem alternativen Gebiet getestet werden, in dem der Differential Split-Sample Test durchgeführt werden kann. Dies ist meistens der Fall, wenn es sich nicht um klimatische Veränderungen, sondern beispielsweise um Änderungen in der Landnutzung handelt. In diesem Falle sollte ein bemessenes Gebiet gefunden werden, in dem eine ähnliche Landnutzungsänderung stattgefunden hat. Die Kalibrierung sollte in diesem Gebiet mit originaler Landnutzung erfolgen und die Validierung auf den Daten mit neuer Landnutzung.

Wenn alternative Gebiete verwendet werden, sollte mindestes zwei derartige Gebiete identifiziert werden. Das Modell wird für beide Gebiete kalibriert und validiert. Die Validierung ist nur dann erfolgreich, wenn die Ergebnisse für beide Gebiete ähnlich sind. Dabei muss beachtet werden, dass der Differential Split-Sample Test im Gegensatz zum Proxy - Basin - Test für beide Gebiete unabhängig durchgeführt wird.

Proxy-basin Differential Split-Sample Test

Wie bereits der Name suggeriert ist dieser Test die Verbindung aus Proxy-basin und Differential Split-Sample Test und sollte dann angewendet werden, wenn ein Modell räumlich übertragbar sein soll und unter veränderten Bedingungen angewendet wird.

Voraussetzung für die Modellkalibrierung mit JAMS

Um ein Modell zu kalibrieren, müssen mehrere Voraussetzungen gegeben sein:

• das Modell muss funktionsfähig sein
• es muss mindestens eine gemessene/beobachtete Zeitreihe vorliegen, die mit den Modellergebnisse verglichen werden kann
• für die Quantifizierung muss ein Bewertungskriterium im Modell berechnet werden. Die Berechnung sollte mit dem UniversalEfficienyCalculator erfolgen. Eine Anleitung zum Einfügen dieser Komponente ist im Tutorium Einrichten von Bewertungskriterien zu finden.

Modellkalibrierung mit JAMS

Um eine vorhandenes Modell mit integrierter Berechnung der Bewertungskriterien zu kalibrieren, gibt es zwei gängige Möglichkeiten.

Achtung: Durch zahlreiche Änderungen mit der neuen Version von JAMS-3 steht derzeit nur die Offline Kalibrierung zur Verfügung

Offline Kalibrierung

Erstens ist es möglich eine Kalibrierung lokal auf dem eigenen Computer vorzunehmen. Dies belegt allerdings für einen längeren Zeitraum Rechenresourcen.

Schritt 1

Öffnen Sie den JAMS User Interface Model Editor (JUICE). Laden Sie nun das Modell, dass Sie kalibrieren möchten. Sie sollten nun in etwa folgende Ansicht sehen

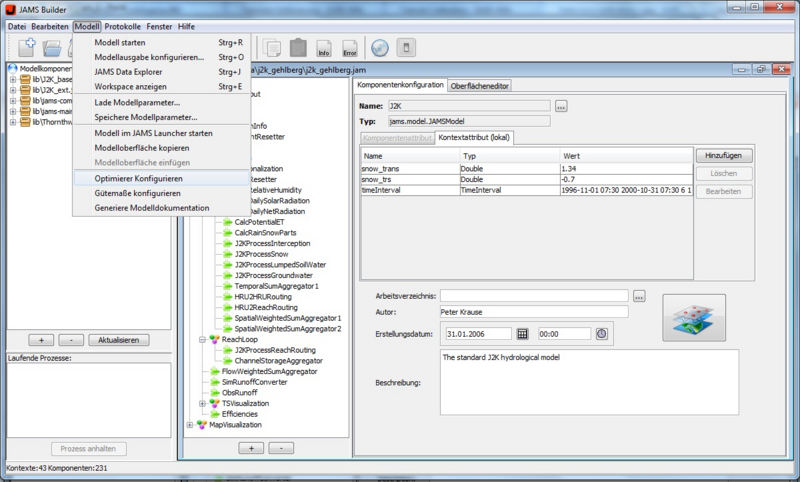
Schritt 2

Wählen Sie nun im Menü Modell den Eintrag Optimierer konfigurieren. Es sollte sich nun ein Dialogfenster öffnen, der die Konfiguration der Kalibrierung ermöglicht. Der Dialog ist dreifach gegliedert. Im oberen Bereich kann der Optimierer/Sampler konfiguriert werden. Im linken unteren Bereich befindet sich nun das Feld zur Parameterkonfiguration und im rechten unteren Bereich werden Bewertungskriterien / Zielfunktionen selektiert.

Wir beginnen mit der Auswahl und Konfiguration des Optimierungsverfahrens:

einkriterielle Optimierungsverfahren

• Shuffled Complex Evolution (SCE)
• Branch and Bound
• Nelder Mead
• DIRECT
• Gutmann Method
• Gaußprozessoptimierer
• Parallelisiertes SCE

mehrkriterielle Optimierungsverfahren

• NSGA-2
• MOCOM

Stichprobengeneratoren

• Random Sampling
• Latin Hypercube Random Sampler
• Parallelisierter Stichprobengenerator

Eine Beschreibung aller Verfahren und deren Eigenschaften ist hier zu finden. Für die Anwendung mit einem einzelnen Zielkriterium hat sich das Shuffled Complex Evolution (SCE) als empfehlenswert herausgestellt. Das Verfahren findet mit hoher Wahrscheinlichkeit eine global optimale Parametrisierung. SCE benötigt nur einen Parameter: die Anzahl der Komplexe. Dieser Parameter steuert ob der Parametersuchraum eher breit gefächert durchsucht wird oder sich das Verfahren schnell auf ein (unter Umständen lokales) Minimum konzentriert. Meist kann mit dem Standardwert 2 gearbeitet werden. Für die multikriterielle Optimierung liefert NSGA - 2 sehr gute Ergebnisse. In unserem Beispiel verwenden wir SCE.

Wichtige Hinweise:

• für die Sensitivitäts- und Unsicherheitsanalyse benötigen Sie Stichprobengeneratoren.
• eine multikriterielle Kalibrierung liefert in der Regel bessere Ergebnisse als eine einkriterielle Kalibrierung. Lesen Sie hierzu den Abschnitt einkriteriell vs. multikriteriell

• setzen Sie die maximale Anzahl von Iterationen ausreichend hoch. Zeichnet sich ab, dass eine Optimierung bereits konvergiert, bevor die max. Anzahl von Modellausführungen erreicht wurde, lässt sie sich zu jedem beliebigen Zeitpunkt stoppen. Eine abgeschlossene Optimierung lässt sich nicht fortsetzen, sondern muss neu gestartet werden, was evtl. unnötig Zeit kostet.

• verfügen Sie über einen Parallelrechner oder einen Rechner mit mehreren Cores, sollten Sie die parallele Ausführung nutzen. Setzen Sie hierzu parallelExecution=true und spezifizieren sie den Parameter threadCount entsprechend

• stellen Sie sicher, dass Kalibrierungs- und Validierungszeitraum korrekt spezifiziert sind

• die meisten Modelle benötigen einige Zeit, um die Wasserspeicher zu füllen. Planen Sie daher einen Initialisierungszeitraum vor dem Kalibrierungszeitraum ein. Falls hierfür keine Daten vorhanden sind, können Sie hierzu auch virtuelle Daten verwenden (indem z.B. vorhandene Daten dupliziert werden)

Schritt 3

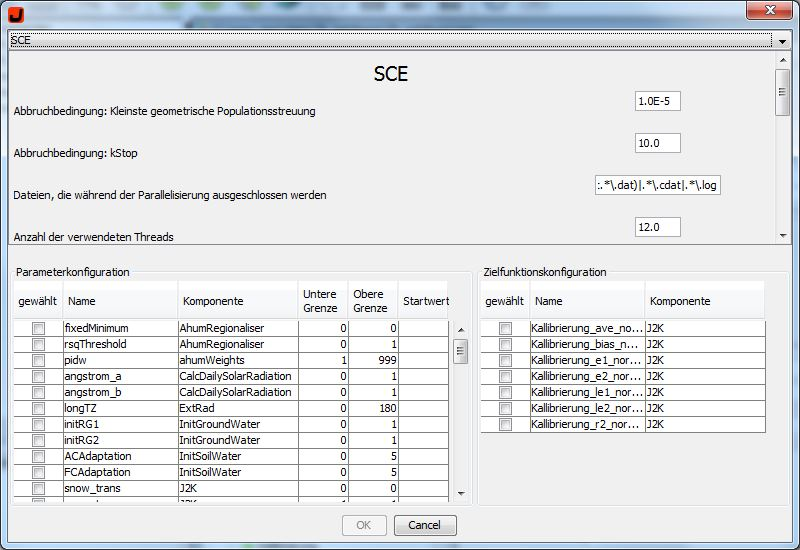
In der Parameterkonfiguration können Sie die Parameter, die optimiert werden sollen, auswählen und gegebenenfalls die Unter und Obergrenze ihren Vorstellungen entsprechend ändern. In der letzten Spalte befindet sich noch die Möglichkeit den Startwert manuell festzulegen mit dem das Programm arbeiten soll. Beachte: In der aktuellen Version ist es nicht möglich, bei der Auswahl mehrerer Parameter, einen Startwert für einen bestimmten Parameter zu wählen und die restlichen Parameter mit Ober- und Untergrenze zu belassen. Es müssen entweder alle Parameter einen Startwert oder eine Ober und Untergrenze besitzen.

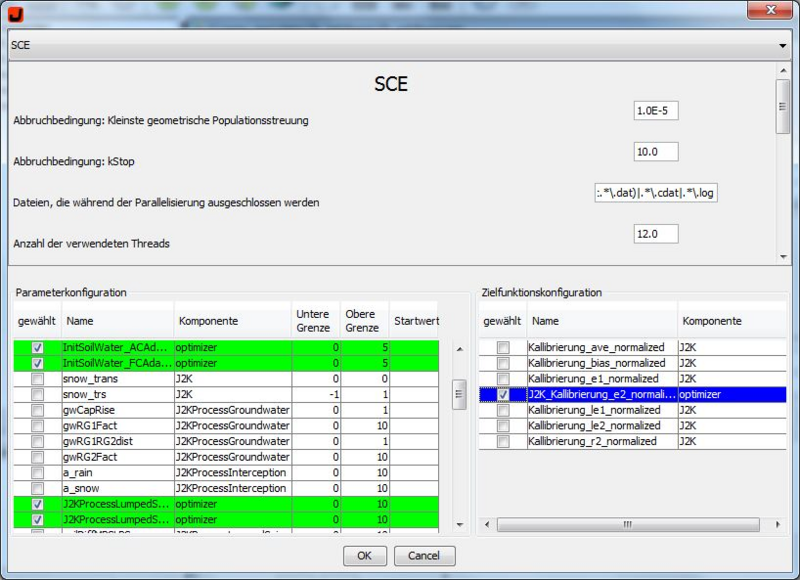
In unserem Beispiel verwenden wir die Parameter: soilConcRD1, soilConcRD2, soilLinRed, FCAdaptation, ACAdaptation, baseTemp ohne Starwerte.
Die unter dem Schritt Voraussetzung festgelegten Gütekriterien sollten nun in dem unteren rechten Bereich eingeschrieben sein. Hier können nun ebenfalls einzelne Kriterien ausgewählt werden um die Optimierung individuell nach Bedarf anzupassen. In unserem Fall das Kriterium: kallibrierung_ec2_normalized.

Eine Einführung in die Kalibrierungsparameter der Modelle J2000 und J2000g ist hier und hier zu finden

Wichtige Hinweise:

• das gewählte Bewertungskriterium hat entscheidenden Einfluss auf die Optimierung. Treffen Sie diese Wahl sorgfältig.

• Parameter, die nicht sensitiv sind, können durch die Kalibrierung nicht identifiziert werden. Überlegen Sie daher, ob Sie diese Parameter kalibrieren wollen.

Schritt 4

Sind die Voreinstellungen getroffen klicken Sie auf OK und starten den Optimierungsprozess über den Button Run Model. Im linken unteren Teil des JAMS Builders erscheint nun unter Laufende Prozesse der Optimierungsvorgang.

Wichtige Hinweise:

• Der Optimierungsassistent fügt automatisch die gewählten Parameter und Bewertungsfunktionen zur Liste der Modellausgaben hinzu. Alle anderen Gütekriterien und Modellzustände werden nicht automatisch ausgegeben. Sollen diese auch herausgeschrieben werden, so fügen Sie diese manuell in der Funktion <it>Modellausgaben</it> hinzu. ACHTUNG: Achten Sie darauf, dass sich die Attribute im korrekten Kontext befinden. Gütekriterien sollten sich beispielsweise immer in Kontext des Optimierers befinden.

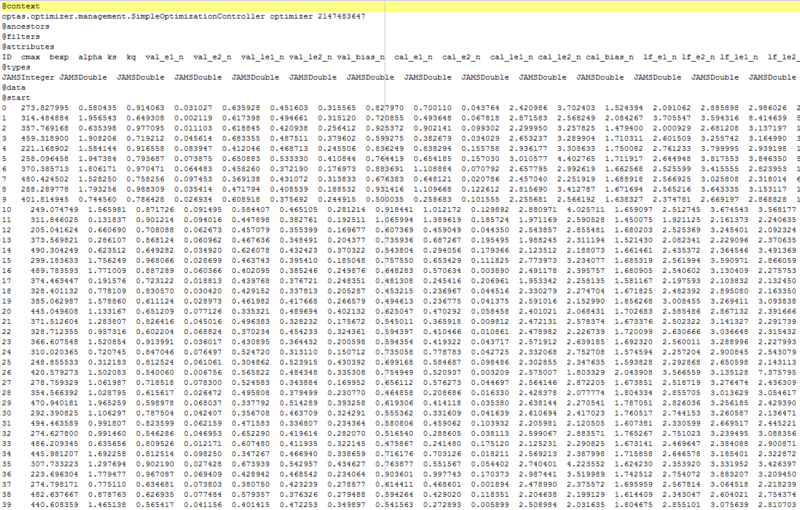
Schritt 5 Sobald die Kalibrierung läuft, wird im Ausgabeverzeichnis des Modellarbeitsverzeichnisses ein Datei mit dem Namen <it>optimization_wizard_optimizer.dat</it> angelegt. In dieser Datei werden für jede Modelliteration die verwendeten Parameter und die erzielten Bewertungskriterien gespeichert. Die Datei sollte in etwa wie folgt aussehen:

Laden Sie diese Datei in ein Tabellenkalkulationsprogramm (z.B. Excel). Sie können nun die Datensätze nach dem optimierten Bewertungskriterium sortieren und die optimale Parametrisierung ablesen.

Online Kalibrierung (nur für JAMS-2 Modelle)

Als Alternative zur Offline Kalibrierung kann dieser Prozess auch über ein Online Portal auf dem Rechencluster des Lehrstuhls für Geoinformatik, Geohydrologie und Modellierung an der Friedrich - Schiller - Universität Jena durchgeführt werden. Dies belegt lokal keine Rechenresourcen und erlaubt die Kalibrierung von bis zu vier Modellen gleichzeitig.

Schritt 1

Öffnen Sie einen Internet Browser (z.B. Firefox) und navigieren sie zu der Website [[1]] Sie sehen nun folgendes Fenster und werden aufgefordert sich anzumelden. Um sich zu registrieren setzen sie sich bitte mit

• Christian Fischer
• christian.fischer.2@uni-jena.de

in Verbindung.

Schritt 2

Nach der Anmeldung sehen sie nun das Hauptfenster der Anwendung.

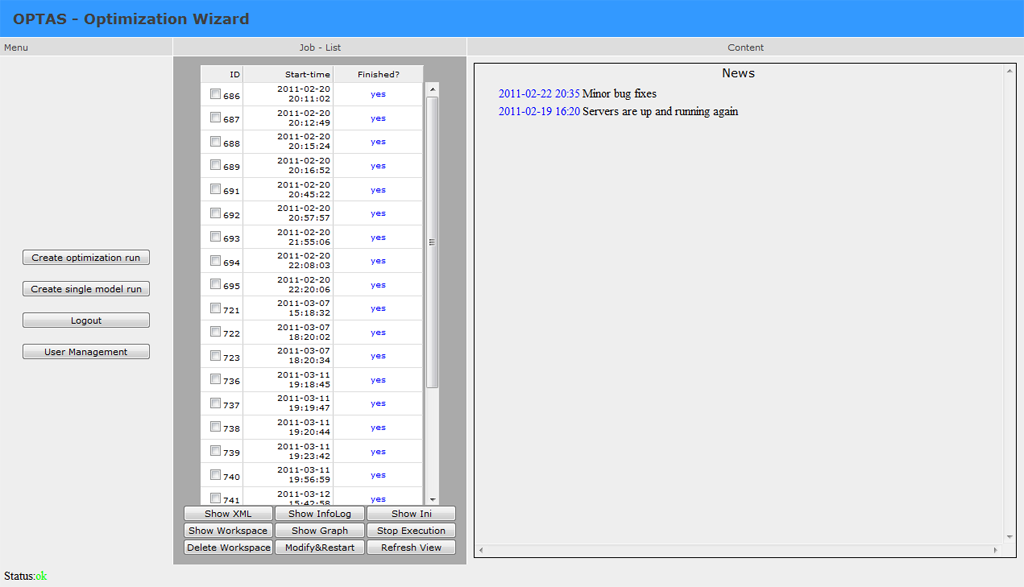
Das Fenster ist dreigeteilt. Im mittleren Teil sehen sie eine Auflistung aller bisher gestarteten Aufgaben. Abgeschlossene Aufgaben werden blau angezeigt und Aufgaben, die sich noch in der Ausführung befinden, werden grün dargestellt. Rot dargestellte Einträgen zeigen, dass während der Konfiguration einer neuen Aufgabe/Kalibrierung ein Fehler aufgetreten ist. Der rechte Bereich des Fensters zeigt verschiedene Inhalte an. Bei Beginn der Anwendung sehen Sie hier Neuigkeiten über das OPTAS - Projekt. Im Allgemeinen werden Informationen bis zu einer Größe von 1 Megabyte direkt angezeigt. Größere Datenmengen werden nicht angezeigt, da dies die Seitendarstellung beeinträchtigt. Statt dessen wird dann mit den Informationen eine gepackte Datei erzeugt und zum Download bereit gestellt.

Schritt 3

Um eine neue Kalibrierung durchzuführen klicken sie auf "Create Optimization Run". Sie gelangen nun zum ersten Schritt des Kalibrierungsprozesses.

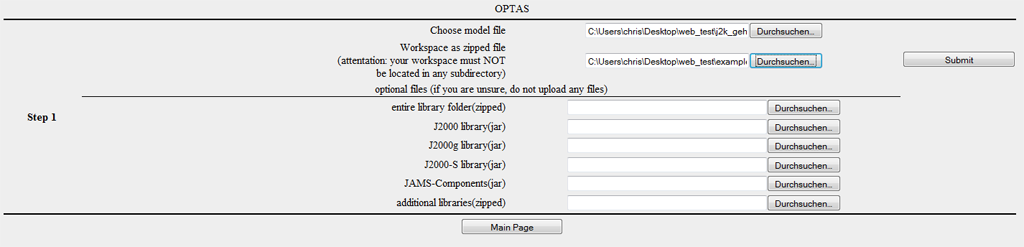
In diesem Schritt werden Sie aufgefordert, die benötigten Daten zur Verfügung zu stellen. Laden Sie nun das zu kalibrierende Modell (jam Datei) in das erste Dateiauswahlfeld. Komprimieren Sie jetzt das Arbeitsverzeichnis des Modells als zip - Archiv. Hierfür eignen sich Packprogramme wie beispielsweise 7-zip. Achten Sie hierbei darauf, dass

• sich das Arbeitsverzeichnis in keinem Unterverzeichnis befinden darf
• sie möglichst keine nicht benötigten Dateien (z.b im Output Verzeichnis hochladen) hochladen. Der Upload ist auf 20mb limitiert.
• sich die Datei default.jap nicht im Arbeitsverzeichnis befindet

Laden Sie nun das komprimierte Arbeitsverzeichnis in das zweite Dateiauswahlfeld. Das Modell wird standardmäßig mit einer aktuellen JAMS/J2000 Version ausgeführt. Bibliotheken zu J2000g und J2000-S sind ebenfalls standardmäßig vorhanden, so dass Sie für die meisten Anwendungen keine weiteren Dateien angeben müssen.
Benötigen Sie allerdings speziell angepasste Versionen der Komponentenbibliotheken zu den Modellen J2000, J2000-S oder J2000g, so laden Sie diese (nicht gepackt) in die entsprechenden Dateiauswahlfelder. Falls Ihr Modell noch weitere Bibliotheken benötigt, können Sie diese als zip-Archiv gepackt in dem entsprechenden Dateiauswahlfeld angeben. Klicken Sie zum Abschluss auf Submit. Die von Ihnen angegeben Dateien werden nun auf die Serverumgebung geladen. Der Managementserver (Sonne) prüft die verfügbaren Arbeitsrechner auf freie Rechenkapazitäten und weist ihren Task einem Arbeitsrechner zu.

Schritt 4

Nachdem das Modell und der Workspace übertragen wurden, wird folgender Dialog zur Auswahl von Parametern und Zielkriterien angezeigt.

Die erste Liste zeigt alle potentiellen Parameter des Modells. Wählen Sie aus der Liste diejenigen Parameter aus, die Sie kalibrieren möchten. Wenn Sie mehrere Parameter markieren wollen, halten Sie die STRG-Taste gedrückt, während Sie mit der Maus die Markierung vornehmen. Im unteren Abschnitt des Dialoges wird die Zielfunktion spezifiziert. Hierbei kann entweder ein einzelnes Kriterium ausgewählt werden oder aber auch mehrere Kriterien (dabei STRG Taste gedrückt halten). Bei der Auswahl mehrere Kriterien erzeugt man ein multikriterielles Optimierungsproblem, das sich hinsichtlich seiner Lösungseigenschaften wesentlich von einem einkriteriellen (gewöhnlichen) Optimierungsproblem unterscheidet. Da auch nicht jede Optimierungsmethode für multikriterielle Probleme geeignet ist, stehen in diesem Fall nicht alle Optimierer zur Verfügung.

Schritt 5

In diesem Schritt soll für jeden Parameter der gültige Wertebereich festgelegt werden. Für jeden ausgewählten Parameter steht ein Eingabefeld für die Spezifikation von unteren und oberen Schranken zur Verfügung. Die Felder sind mit default-Werten vorbelegt, sofern für diese für den Parameter zur Verfügung stehen. Diese Standardwerte sind meist sehr weit gefasst, so dass empfohlen wird, eine Weitere Einschränkung vorzunehmen. Es besteht außerdem optional die Möglichkeit einen Startwert anzugeben. Dies ist sinnvoll, falls bereits ein guter Parametersatz bekannt ist, der Ausgangspunkt der Kalibrierung sein soll.

Im zweiten Teil dieses Schrittes haben Sie außerdem die Möglichkeit für jedes gewählte Kriterium festzulegen, ob das Kriterium

• minimiert (Beispiel RSME - root square mean error) ,
• maximiert (Beispiel r²,E1,E2,logE1,logE2),
• absolut minimiert (d.h min |f(x)| z.B für den absoluten Volumenfehler) ,
• oder absolut maximiert werden soll.

Die nachfolgenden Abbildung zeigt den entsprechenden Dialog. Hierbei wurden die Parameter des Schneemoduls gewählt und die Default-Grenzen eingetragen.

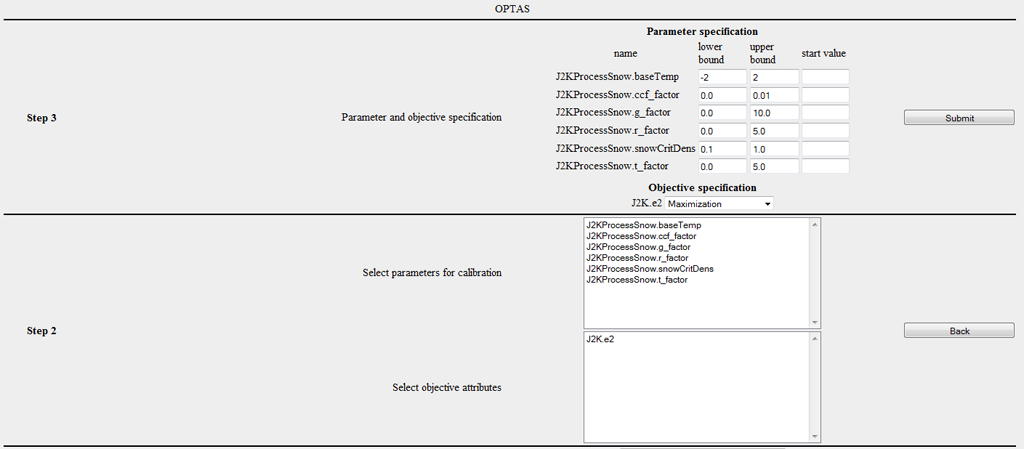
Schritt 6

Sie werden nun aufgefordert, das gewünschte Optimierungsverfahren zu wählen. Derzeit stehen folgende Verfahren zur Auswahl:

• Shuffled Complex Evolution (Duan et al., 1992)
• Branch and Bound (Horst et al., 2000)
• Nelder Mead
• DIRECT (Finkel, D., 2003)
• Gutmann Method (Gutmann .. ?)
• Stichprobengenerator (Random Sampling)
• Latin Hypercube Random Sampler
• Gaußprozessoptimierer
• NSGA-2 (Deb et al., ?)
• MOCOM ()
• Parallelisierter Stichprobengenerator
• Parallelisiertes SCE

Für die meisten einkriteriellen Anwendungen kann das Shuffled Complex Evolution (SCE) Verfahren und das DIRECT Verfahren empfohlen werden. Für multikriterielle Aufgabenstellungen liefert NSGA-2 meist hervorragende Ergebnisse.

Schritt 7

Vieler Optimierer lassen sich auf die Problemstellung angepasst parametrisieren. SCE besitze einen frei wählbaren Parameter: die Anzahl der Komplexe. Ein kleiner Wert führt zu einer schnelleren Konvergenz, allerdings mit höherem Risiko die globale Lösung nicht zu identifizieren, während ein großer Wert die Rechenzeit deutlich erhöht, aber die Wahrscheinlichkeit zum Auffinden des Optimums stark verbessert. Meist kann mit dem Standardwert 2 gearbeitet werden. (Literatur?) Dem gegenüber besitzt DIRECT beispielsweise keine Parameter. ein sehr robustes Verhalten zeigt und keine Parametrisierung des Verfahrens erforderlich ist. Desweiteren stehen unabhängig vom Verfahren drei Check - Boxen zur Verfügung.

• remove not used components: Entfernt Komponenten aus der Modellstruktur von denen gesichert ist, dass sie das Kalibrierungskriterium nicht beeinflussen
• remove GUI-components: Entfernt alle grafischen Komponenten aus der Modellstruktur. Diese Option wird stark empfohlen, da z.B Diagramme die Effizienz der Kalibrierung stark negativ beeinflussen
• optimize model structure: ist derzeit ohne Funktion

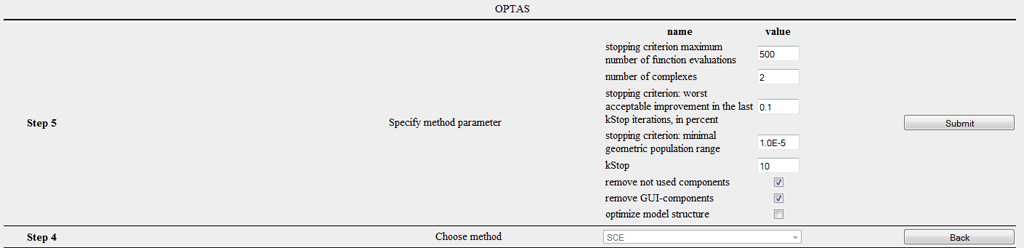
Die folgende Abbildung zeigt Schritt 7 zur Konfiguration des SCE Verfahrens.

Schritt 8

Bevor Sie die Optimierung starten, können Sie nun angeben, welche Variablen/Attribute des Modells ausgegeben werden können. Standardmäßig werden bereits die gewählten Parameter und Zielkriterien ausgegeben, so dass unnötig ist diese manuell hinzuzufügen. Bitte beachten Sie aber, dass die Abspeicherung von zeitlich und räumlich varierende Attributen (z.B. outRD1 für jede HRU) sehr groß werden kann und evtl. die Speicher-Quote für ihren Benutzeraccount überschreitet.

Schritt 9

Sie erhalten nun eine Zusammenfassung der automatisch vorgenommenen Modifikationen. Sie bekommen insbesondere aufgelistet, welche Komponenten als irrelevant klassifiziert wurden. Mit einem Klick auf Submit starten Sie den Optimierungsprozess.

OPTAS Bedienung

Nachdem Sie nun die Kalibrierung eines Modells gestartet haben, sollten Sie auf der Hauptseite einen neuen Job sehen. Dieser wird in grün dargestellt um anzudeuten, dass die Ausführung noch nicht beendet ist. Sie sehen außerdem die ID, das Startdatum und das geschätzte Fertigstellungsdatum dieser Optimierung. Wenn Sie den erzeugten Auftrag selektieren stehen Ihnen nun mehrere Aktionen zur Verfügung.

Show XML

Sie können sich die automatisch erzeugte Modellbeschreibung anzeigen lassen mit der dieser Auftrag ausgeführt wird. Sobald Sie die Schaltfläche betätigen erscheint diese im Inhaltsfenster auf der rechten Seite und kann von dort auch heruntergeladen werden.

Show Infolog

Betätigen Sie diese Schaltfläche um sich die Statusmeldungen des laufenden Modells anzeigen zu lassen. Bei einer Offline Ausführung des Modells werden diese Informationen in die Datei info.log bzw. error.log geschrieben.

Show Ini

Die Optimierung-Ini Datei enthält alle vorgenommen Einstellungen und fasst diese in Kurzschreibweise zusammen. Diese Funktion orientiert sich an dem fortgeschrittenen Benutzer bzw. Entwickler, so dass hier auf eine detailierte Erläuterung verzichtet wird.

Show Workspace

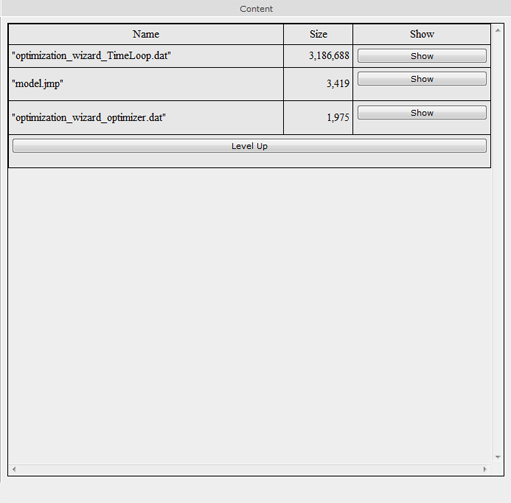
Diese Funktion listet alle Dateien und Verzeichnisse im Workspace auf. Durch einen Klick auf das Verzeichnis/Datei kann dessen Inhalt angezeigt werden. Die Modellergebnisse lassen sich normalerweise im Ordner /current/ finden, den die folgende Abbildung beispielhaft zeigt.

Hierbei ist zu beachten, dass Dateiinhalte nur bis zu einer Maximalgröße von 1 Megabyte dargestellt werden und ansonsten als zip Datei gepackt zum Download zur Verfügung gestellt werden.

Show Graph

Abhängigkeiten zwischen verschiedenen JAMS-Componenten eines Modells können grafisch dargestellt werden. Diese Funktion erzeugt einen gerichteten Graphen, dessen Knoten die Menge aller Komponenten des Modells sind. In diesem Graphen ist eine Komponente A mit einer Komponente B verknüpft, wenn A von B abhängig ist, in dem Sinne, dass B Daten erzeugt, die direkt von A benötigt werden. Außerdem werden alle Komponenten rot dargestellt, die während der Modellkonfiguration entfernt wurden. Dieser Abhängigkeitsgraph erlaubt die Analyse komplexerer Abhängigkeitsbeziehungen, wie zum Beispiel die Bestimmung von Komponenten, die indirekt abhängig von einem bestimmten Parameter sind. Derartige Analysen sollten jedoch automatisiert durchgeführt werden. Die grafische Ausgabe dieses Graphen dient vorrangig der Veranschaulichung.

Stop Execution Beendet die Ausführung eines oder mehrere Modelläufe.

Delete Workspace Löscht das komplette Arbeitsverzeichnis des Modells auf der Serverumgebung. Bitte verwenden Sie diese Funktion, wenn die Optimierung abgeschlossen ist und sie die Daten gespeichert haben. Die entlastet die Serverumgebung und beschleunigt die Darstellung der OPTAS Umgebung.

Modify & Restart Diese Funktion richtet sich an den fortgeschritten Benutzer. Oft wird ein Neustart eines Modells oder Kalibrierungsaufgabe benötigt, ohne dass große Änderungen der Konfiguration nötig sind. Durch die Funktion Modify & Restart, kann die Konfigurationsdatei der Optimierung direkt verändert werden und anschließend der Neustart des Modells in einem neuen Arbeitsverzeichnis erzwungen werden.

Refresh View Aktualisiert die Ansicht. Bitte Verwenden Sie nicht die Aktualisierungsfunktion ihres Browsers (meist F5), da dies eine erneute Ausführung des letzten Befehls nach sich ziegt (z.B. Start des Modells)