Modelo Hidrológico J2000

O sistema modelo hidrológico J2000 oferece uma modelagem física baseada no balanço hídrico de grandes bacias hidrográficas. Além da simulação dos processos hidrológicos, que influenciam o escoamento e a sua concentração nas escalas meso-superior e macro, o sistema de modelagem contém rotinas que ajudam a regionalizar os valores pontuais climáticos disponíveis e valores de precipitação com bastante segurança. Além disso, o cálculo da evaporação real, com a qual o cálculo é efetuado levando-se em conta diferenças de área e o comportamento da evaporação das classes de uso da terra, está integrado no modelo. Uma vez que o modelo deve ser adequado para a modelação de grandes áreas de captação de mais de 1000 km ², assegura-se que a modelação pode ser efetuada por meio dos dados de base disponíveis em escala nacional. A simulação de diferentes processos hidrológicos é realizada nos módulos de programa que são preenchidos e, tanto quanto possível de forma independente do outro. Essa oferece para editar, substituir ou adicionar módulos individuais sem a necessidade de estruturar o modelo inteiro de novo. O escoamento total modelado é acumulado a partir da soma dos componentes individuais de escoamento que são calculados separadamente durante a modelação. O sistema de modelagem diferencia-se entre quatro componentes de escoamento de acordo com a sua origem específica. O componente com maior dinâmica temporal é o escoamento rápido e direto (RD1). Ele consiste no escoamento de áreas fechadas, de água da neve, que drena dentro de camadas de neve, e do escoamento superficial quando as áreas de saturação se desenvolvem. O componente de escoamento lento direto (RD2), o qual pode ser considerado similar ao escoamento hipodérmico lateral dentro da zona do solo, reage insignificantemente de forma mais lenta. Dois componentes adicionais de escoamento de base podem ser distinguidos. Por um lado, existe o componente de escoamento rápido de base (RG1) que simula o escoamento de zonas intempéries bem permeáveis de perto da superfície. Por outro lado, existe um componente de escoamento de base lento (RG2), que resulta em escoamento do aquífero conjunto ou aquífero de rocha homogénea solta. A repartição da água de precipitação para os componentes individuais de escoamento é realizada no modelo com base em parâmetros de área, que podem ser derivados a partir dos dados de base aplicado. Além da forma de relevo, parâmetros do solo específicos, como a condutividade hidráulica de horizontes individuais, têm uma influência importante. O cálculo dos diferentes tempos de concentração dos componentes de escoamento é realizado tendo-se em consideração as características hidráulicas dos armazenamentos em que os componentes individuais escoam. Além disso, as influências de variáveis ​​como a humidade precedente da área são considerados durante a modelagem.

Índice 1 GUI 2 Arquivos de entrada 2.1 Dados 2.2 Parâmetros 3 Regionalização dos dados de clima e de precipitação 3.1 Processamento Geral 3.2 Método de correção específico e o método de cálculo para os conjuntos de dados individuais

GUI

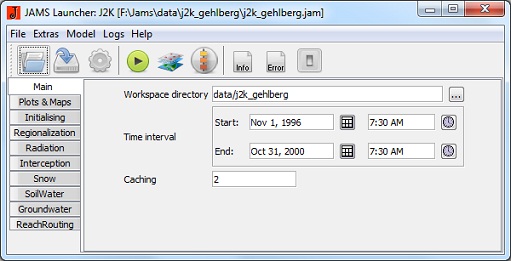
Após iniciar o JAMS, a janela principal abre com vários tabuladores:

Basic Settings

• Diretório Workspace: Define o diretório de trabalho. Tem que conter mais três pastas: Parâmetros (para todos os arquivos de parâmetros), Data (para todos os arquivos de dados) e de Saída (para todos os arquivos de saída).

• Time interval: O intervalo de tempo para a execução do modelo escolhido.

• Caching: Os resultados de alguns processos de computação intensiva podem ser temporariamente armazenados no disco rígido e reutilizados para outras execuções de modelos. Assim, o modelo de execução será ligeiramente mais rápida. Atenção: Esta função não é completamente segura e ainda deve ser aplicada apenas por usuários experientes.

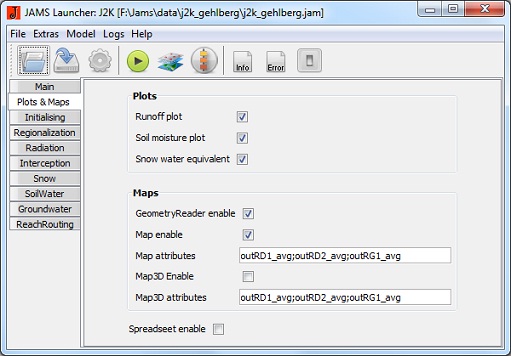
Diagramas e mapas

• Runoff plot: Ativa a visualização gráfica do escoamento modelado e medido durante execução do modelo.

• Soil moisture plot: Ativa a exibição gráfica da umidade do solo relativa durante a execução do modelo.

• Snow water equivalent: Ativa a exibição gráfica do equivalente de água da neve durante a execução do modelo.

• Map enable: Ativa a saída de uma exibição cartográfica de variáveis ​​de estado selecionados.

• Map attributes: Uma lista separada por ponto-e-vírgula de variáveis ​​de estado que serão cartograficamente exibidas.

• Map3D enable: Permite uma saída 3D de uma exposição cartográfica de variáveis ​​de estado selecionadas.

• Map3D attributes: Uma lista separada por ponto-e-vírgula de variáveis ​​de estado que serão cartograficamente exibidas (em 3D).

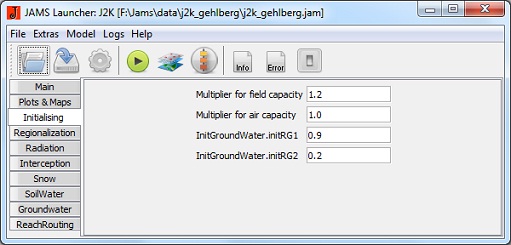
Inicialização

• Multiplier for field capacity: A capacidade máxima de armazenamento dos reservatórios de poros médios (MPS) pode ser aumentada (valor > 1) ou diminuído (valor < 1).

• Multiplier for air capacity: A máxima capacidade de armazenamento dos reservatórios de poros grandes (LPS) pode ser aumentada (valor > 1) ou diminuída (valor < 1).
• InitRG1: enchimento relativo do armazenamento de águas subterrâneas superior no início da execução do modelo (1 lotado, 0 vazio).

• InitRG2: enchimento relativo do armazenamento inferior de águas subterrâneas no início da execução do modelo (1 lotado, 0 vazio).

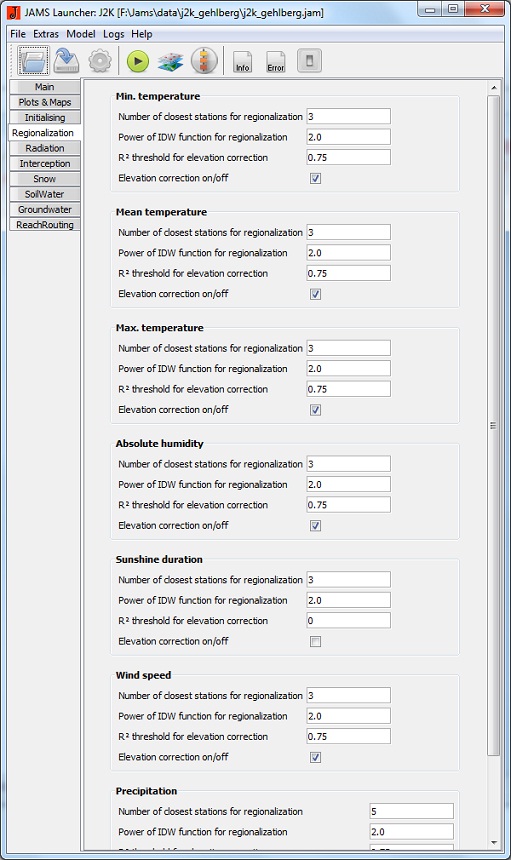
Regionalização

• number of closest stations for regionalization: n número de estações utilizadas para calcular o valor de um HRU (n estações que estão mais próximas do HRU são selecionados).

• Power of IDW function for regionalization: Fator de ponderação usado ​​para exponenciar a distância de cada estação para a HRU respectiva.

• elevation correction on/off: Ativa a correção de elevação dos valores de dados.

• r-sqrt threshold for elevation correction: valor limite para a correção de elevação dos valores de dados. Se o coeficiente de determinação da relação de regressão entre os dados medidos das estações e elevações de estação for menor do que este valor, uma correção de elevação não será realizada.

Essas configurações (por exemplo, a temperatura mínima, a máxima, a temperatura média do ar, a precipitação, a humidade absoluta do ar, a velocidade do vento, a duração da luz solar) podem ser ajustadas para cada variável de entrada única.

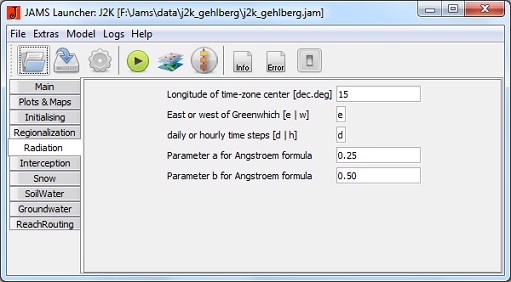
Radiação

• flowRouteTA [h]: tempo de execução da rota de escoamento

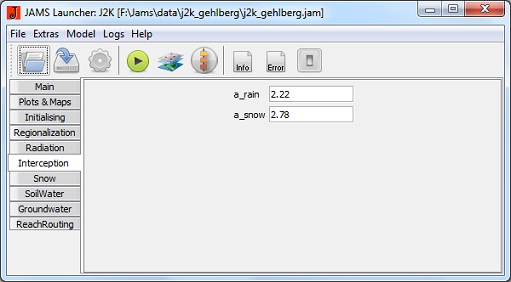
Intercepção

• a_rain [mm]: a capacidade máxima de armazenamento do reservatório de interceptação por m² de área foliar para a chuva

• a_snow [mm]: a capacidade máxima de armazenamento do reservatório de interceptação por m² de área foliar para a neve

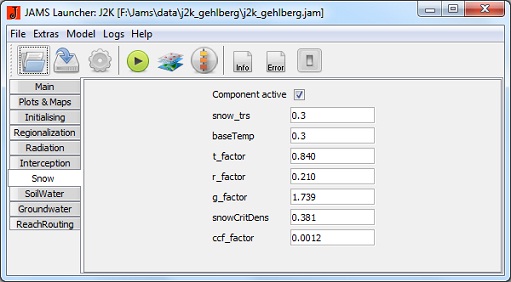
Neve

• Component active: Ativa o módulo de neve.

• baseTemp [°C]: valor limite da temperatura para a precipitação da neve.

• t_fator [mm/°C]: fator de temperatura para cálculo do escoamento de neve derretida.

• r_fator [mm/°C]: fator de chuva para o cálculo do escoamento da neve derretida.

• g_fator [mm]: Solo fator de fluxo de calor para o cálculo do escoamento neve derretida.

• snowCritDens [g/cm³]: densidade crítica da neve

• ccf_fator [-]: fator para o cálculo do conteúdo frio da cobertura de neve

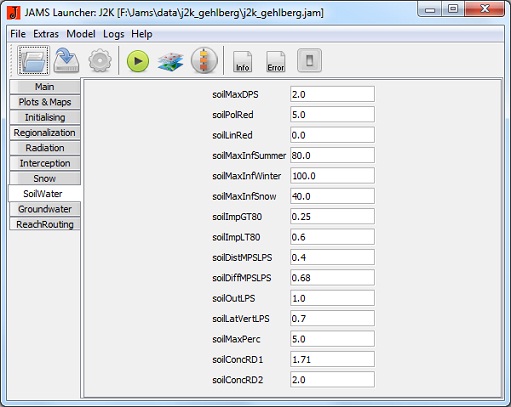
Soilwater

• MaxDPS [mm]: reserva vazia máxima

• PolRed [-]: fator de redução polinomial para a redução da evaporação potencial com abastecimento de água limitado.

• LinRed [-]: fator de redução linear para redução da evaporação potencial com abastecimento de água limitado.

(Nota: PolRed e LinRed não representam alternativas. Apenas a um deles pode ser atribuído um valor, o outro tem de ser 0.)

• MaxInfSummer [mm]: a infiltração máxima durante o período de verão

• MaxInfWinter [mm]: infiltração máxima durante o período de inverno

• MaxInfSnow [mm]: infiltração máxima com cobertura de neve

• ImpGT80 [-]: capacidade de infiltração relativa de áreas com um grau de vedação > 80%

• ImpLT80 [-]: capacidade de infiltração relativa de áreas com um grau de vedação < 80%

• DistMPSLPS [-]: coeficiente de calibração para a distribuição de infiltração em reservatórios do solo LPS e MPS

• DiffMPSLPS [-]: coeficiente de calibração para a definição do valor da difusão de reservatório LPS em relação ao MPS no final de um intervalo de tempo

• OutLPS [-]: coeficiente de calibração para a definição do fluxo de saída do LPS

• LatVertLPS [-]: coeficiente de calibração para a distribuição do fluxo de saída do LPS na lateral (interfluxo) e vertical (percolação) do componente

• MaxPerc [mm]: Taxa máxima de percolação

• ConcRD1 [-]: coeficiente de retenção para o escoamento direto

• ConcRD2 [-]: coeficiente de retenção para interfluxo

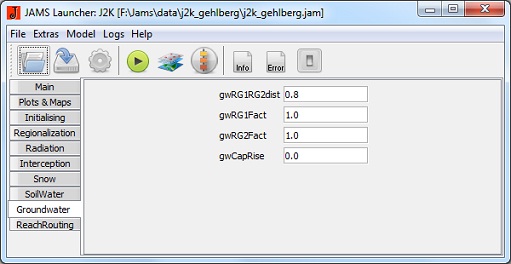
Água Subterrânea

• RG1RG2dist [-]: coeficiente de calibração para a distribuição de água de percolação

• RG1Fact [-]: fator de dinâmica de escoamento do RG1

• RG2Fact [-]: fator de dinâmica de escoamento da RG2

• CapRise [-]: fator para a definição de ascensão capilar

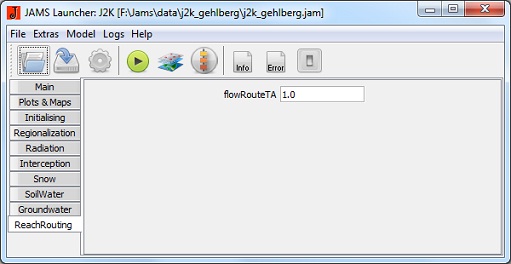
Roteamento no fluxo

• flowRouteTA [h]: tempo de execução da rota de escoamento

Quando todos os parâmetros estiverem definidos, a modelagem é iniciada através do botão [Run]. Uma janela se abre com tabuladores diferentes.

A guia [JAMSProgress] representa informações gerais sobre a execução do modelo atual em forma de texto. Se um erro ou problema ocorrer durante a execução, uma mensagem de erro possivelmente aparece nesta visão. Além disso, vários critérios de eficácia são apresentados após a conclusão da execução do modelo. Estes são os seguintes:

e2 ... Nash-Sutcliff-efficiency com potência 2 (forma clássica)

e1 ... Nash-Sutcliff-efficiency modificada (diferenças não são quadrados, mas seus valores absolutos são aplicados)

log_e2 ... Nash-Sutcliff-efficiency modificada (o logaritmo dos valores são considerados)

log_e1 ... Nash-Sutcliff-efficiency modificada (o logaritmo dos valores são tomados; diferenças não são quadrados, e sim seus valores absolutos são aplicados)

ioa2 ... índice de concordância de acordo com a Willmot

ioa1 ... índice modificado de concordância de acordo com Willmot (diferenças não são quadrados)

r² ... coeficiente de determinação

grad ... declive da linha de regressão

wr² ... coeficiente de determinação, ponderado com o declive da linha de regressão

dsGrad ... gradiente de soma dupla

AVE ... erro de volume absoluto

RSME ... erro médio de raíz quadrático

pbias ... erro de volume relativo percentual

As outras guias contêm as parcelas e mapas selecionados previamente.

---

Arquivos de entrada

Arquivos de entrada são os parâmetros temporais estáticos, assim como temporais de dados de entrada (valores variáveis ​​de clima, os valores de precipitação, os valores de escoamento). Estes são lidos como arquivos ASCII.

Geralmente, para todos os aquivos de entrada, é necessário que:

• o separador seja o tabulador
• o separador decimal seja o ponto

Dados

O sistema de modelagem J2000 espera que os seguintes arquivos de dados para a inicialização do modelo:

Nome	Descrição	Unidade
ahum.dat	umidade absoluta	g/cm 3
orun.dat	passagem do fluxo medida no segundo escoamento	m 3/s
rain.dat	quantidade medida de precipitação	mm
rhum.dat	umidade relativa	%
sunh.dat	duração da luz solar	h
tmax.dat	temperatura máxima	° C
tmean.dat	temperatura média do ar	° C
tmin.dat	temperatura mínima	° C
wind.dat	velocidade do vento	m/s

Cada arquivo de dados tem a seguinte estrutura (demonstrado aqui pelo exemplo da chuva):

Linha	width="70%"	Descrição
#rain.dat chuvas
@dataValueAttribs
rain 0 9999 mm	nome da série de dados, o menor valor possível, o maior valor possível, a unidade
@dataSetAttribs
missingDataVal -9999	Valor para marcar valores de dados em falta
dataStart 01.01.1979 7:30	data e hora do primeiro valor de dados
dataEnd 31.12.2000 7:30	data e hora do último valor de dados
tres d	resolução temporal dos dados (aqui: dias)
@statAttribVal
name stat1 stat2	nomes das estações de medição
ID 1574 1513	nome numérico das estações de medição (ID)
elevação 525 498	elevação da estação 1, elevação da estação 2
x 4402310 4422269	Posicionamento oriental da estação1, Posicionamento oriental da estação 2
y 5620906 5616856	Posicionamento setentrional da estação 1, Posicionamento setentrional da estação 2
dataColumn 1 2	número da coluna em particular na parte de dados
@dataVal	parte de dados inicial
01.01.1979 07:30 0.8 0.1	data, hora, valor da estação 1, valor da estação 2
...
31.12.2000 07:30 1.1 0	data, hora, valor da estação 1, valor da estação 2
fim da parte de dados |

Parâmetros

O J2000 espera os arquivos de parâmetros a seguir para a inicialização do modelo:

• landuse.par - uso da terra
• hgeo.par - hidrogeologia
• soils.par - tipos de solo
• reach.par - rede de cursos de água
• hrus.par - parâmetro dos derivados de Unidades de Resposta Hidrológicas (HRUs)

Geralmente, todos os arquivos de parâmetros têm a seguinte estrutura (demonstrado aqui pelo exemplo da rede de cursos de água, veja também a figura da direita):

Linha	width="70%"	Descrição
1	#reach.par
2	nome da variável
3	menor valor possível
maior valor possível |
unidade |
Parte começo de dados |
n	#end of reach.par -> marca o fim do arquivo de parâmetro (aqui: o uso da terra)

• landuse.par

Parâmetro	Descrição
LID	ID do uso da terra
albedo	albedo em%
RSC0_1	resistência de superfície mínima para o solo saturado de água em janeiro
...
RSC0_12	resistência de superfície mínima para o solo saturado de água em dezembro
LAI_d1	índice de área foliar (LAI), no início do período de vegetação
...
LAI_d4	índice de área foliar (LAI), no final do período de vegetação
effHeight_d1	altura efetiva da vegetação no início do período de vegetação
...
effHeight_d4	altura efetiva da vegetação no fim do período de vegetação
rootDepth
sealedGrade	grau de vedação

• hgeo.par

Parâmetro	Descrição
GID	ID de hidrogeologia
RG1_max	capacidade máxima de armazenamento do reservatório de água subterrânea superior
RG2_max	capacidade máxima de armazenamento do reservatório de água subterrânea inferior
RG1_k	coeficiente de armazenamento do reservatório de água subterrânea superior
RG2_k	coeficiente de armazenamento do reservatório de água subterrânea inferior

• reach.par

Parâmetro	Descrição
ID	ID da parte do canal
length	comprimento
ID da parte do canal subjacente
slope	declive
rough	valor da rugosidade de acordo com MANNING
Largura |

• soils.par

Parâmetro	Descrição
SID	ID do tipo de solo
depth	espessura do solo
kf_min	coeficiente de permeabilidade mínima
depth_min	profundidade do horizonte acima do horizonte com o menor coeficiente de permeabilidade
kf_max	coeficiente de permeabilidade máxima
cap_rise	variável booleana, que permite (1) ou restringe (0) a ascensão capilar
aircap	capacidade de ar
fc_sum	capacidade de campo utilizável
fc_1 ...22	capacidade de campo utilizável por decímetro de profundidade de perfil

• hrus.par

Parâmetros das dadas Unidades de Resposta Hidrológicas (HRUs)

Parâmetro	Descrição
ID	HRU ID
x
y	Localização setentrional do ponto centróide
elevation	elevação média
area	área
type	tipo de drenagem: a HRU é drenada na HRU (2), a HRU é drenada na parte do canal (3)
to_poly	ID do HRU subjacente
to_reach	ID da parte do canal adjacente
slope	declive
aspect	aspecto
flowlength	Comprimento de fluxo
soilID	ID da classe de solo
landuseID	ID da classe de uso da terra
hgeoID	ID da classe hidrogeológica

Regionalização dos dados de clima e de precipitação

Processamento Geral

1. Cálculo da regressão linear entre os valores diários da estação e a elevação das estações. Assim, são calculados o coeficiente de determinação (r ²) e da inclinação da linha de regressão (b _H) desta relação. Assume-se que o valor (MW) depende linearmente da elevação do terreno (H), de acordo com:

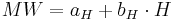
O a_H e o b _H desconhecidos são definidos de acordo com o método de Gauss dos menores quadrados:

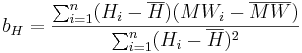
O coeficiente de correlação da regressão é calculado de acordo com a seguinte equação:

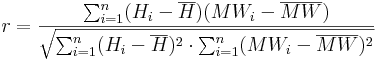
2. Definição de n estações medidoras que estão mais próximas à HRU particular.. O número n que necessita ser introduzido durante a parametrização é dependente da densidade da rede de estações, bem como sobre a posição das estações individuais.

Para cada conjunto de dados, o número de estações (n), que devem ser consideradas para a regionalização deve ser determinado em antemão. Além disso, um fator de ponderação (pIDW) tem de ser fornecido. As n estações mais próximas são definidas de acordo com a regra de cálculo seguinte, com a ajuda das localizações oriental e setentrional (eastings e northings) de todas as estações, bem como as coordenadas da HRU em particular. O primeiro passo consiste em calcular a distância (Dist (i)) de cada estação para a área de interesse:

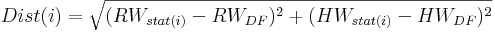
sendo que

RW ...localização oriental da estação i...n, ou a HRU (DF)

HW ...localização setentrional da estação i...n, ou a HRU (DF)

As n estações de com a menor distância à HRU particular são tomadas a partir das distâncias calculadas de acordo com a descrição acima, e são então utilizadas para cálculos posteriores. As distâncias destas estações são convertidas em distâncias ponderadas (wDist(i)), através de potencialização com o fator de ponderação pIDW. Com a ajuda deste fator de ponderação, a influência de estações vizinhas pode ser aumentada e a influência das estações mais afastadas pode ser diminuída. Bons resultados podem ser obtidos com os valores 2 ou 3 para o pIDW.

3. Através de um Inverse-Distance-Weighted (IDW) (Distânica inversa ponderadas), ponderações das n estações são definidas dependentemente de suas distâncias para cada HRU. Através do método IDW a variabilidade horizontal da estação de dados é levada em consideração de acordo com a sua posição espacial. O cálculo é realizado de acordo com a seguinte equação:

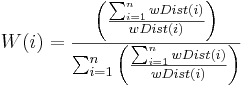
4. O cálculo do valor de dados para cada HRU com as ponderações a partir do ponto 3, e uma correção de elevação opcional para a consideração da variabilidade vertical. A correção de elevação só é realizada quando o coeficiente de determinação (calculado de acordo com o ponto 1) vai além do limite digitado pelo usuário. O cálculo sem a correção de elevação opcional é levada feita de acordo com a seguinte equação:

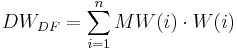
Para os valores de dados que possuem um efeito de elevação, uma correção de elevação para os valores de medição é realizada adicionalmente, quando os valores têm uma relação de regressão estreita (r ² maior do que o valor-limite introduzido pelo usuário). A seguinte equação é aplicada para o cálculo:

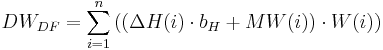
sendo que ΔH(i) ...... diferença de elevação entre a estação i e a HRU

b_H ... declive da linha de regressão

Método de correção específico e o método de cálculo para os conjuntos de dados individuais

Precipitação

Correção do erro de umedecimento e erro de evaporação

A correção do erro de umedecimento e o erro de evaporação é feita de acordo com pesquisas com a ajuda de medidores de precipitação Hellmann como descritos por RICHTER (1995). A fim de oferecer uma correção de erro constante (que resulta da perda de umedecimento e evaporação), funções logarítmicas foram aproximadas separadamente para o semestre de Verão (Maio a Outubro) e semestre de inverno (novembro a abril) com os valores discretos tabulados no sistema de modelação 2000. Se a altura da precipitação ultrapassa o valor de 9 mm, o erro de umedecimento e erro de evaporação são definidos como um valor constante.

O erro de umedecimento e o erro de evaporação para precipitação alturas ≤ 9,0 mm são calculados de acordo com o seguinte equipara:

Para a precipitação alturas >9,0 mm o umedecimento e o erro de evaporação é o seguinte:

Correção do erro provocado pelo vento

A quantificação do erro de precipitação, que é de se esperar é realizada de acordo com a pesquisa de RICHTER (1995) como função da altura da precipitação e da posição da estação. Pressupõe-se que o erro de vento relativo (KR_Wind) para a precipitação de água e também de neve se comporta de forma inversamente proporcional às alturas de precipitação (Pm). O cálculo é realizado de acordo com as seguintes equações:

O cálculo das alturas de precipitação corrigidas para o erro de evaporação e o de vento é então realizada de acordo com a seguinte equação:

Temperatura

O sistema de modelagem J2000 requer valores da temperatura d mínima, bem como a temperatura máxima diária. A partir destes valores, a temperatura média diária (T_mean) é calculada como a média média.

A regionalização dos valores pontuais T_min, T_max e T_mean é realizada de acordo com a regra descrita acima, com correção de elevação opcional.

Velocidade do vento

A velocidade do vento não é dada como valor direto do DWD, mas como observações da força do vento (WS) em Beaufort. A conversão da força do vento para a velocidade do vento a 2 m de altura (v₂) [em ms^-1] pode ser realizada de acordo com a seguinte equação:

Esta conversão tem de ser feita no exterior, porque J2000 espera a velocidade do vento em m/s.

A conversão da velocidade do vento a 2 m de altura a outras alturas - como é exigido em parte durante o cálculo da evaporação e da correção do vento da precipitação - é levada a cabo durante a modelagem de acordo com a seguinte equação:

A interpolação dos valores pontuais para a área é realizada de acordo com o método descrito acima. O sistema de modelagem permite a inclusão da correção de elevação opcional para a regionalização da velocidade do vento. No entanto, esta opção deve ser manuseada com cuidado, uma vez que a velocidade do vento é muito dependente da posição da estação.

Insolação

A insolação diária (S) [em h], é fornecido como valor pelo DWD. A interpolação dos valores de estação para a área é realizada de acordo com o procedimento descrito acima - sem cálculos adicionais ou correções de elevação.

Umidade Relativa

A umidade relativa (U) [em%] pode ser tomada a partir do DWD como valores diários. A regionalização direta dos valores não é recomendada, uma vez que dependem de dois parâmetros: o teor de umidade absoluta e o teor de umidade máxima possível do ar para uma determinada temperatura. Assim, no módulo de regionalização do sistema de modelagem J2000 a umidade absoluta (a) [em g cm^-3] é calculada a partir da umidade relativa e da temperatura na estação. Em seguida, ela é regionalizada e depois a umidade absoluta é convertida para a umidade relativa novamente. Para este propósito, os passos de cálculo são necessários vários que são mostrados abaixo.

'Cálculo da pressão do vapor de saturação

A pressão do vapor de saturação (e_s(T)) [em hPa] é calculada de acordo com a fórmula Magnus com os coeficientes de SONNTAG (1994) para a temperatura do ar (T) [em °C]:

Cálculo da umidade máxima

A umidade máxima (A) é calculada contra a pressão do vapor de saturação (e_s(T)) e a temperatura do ar (T) de acordo com:

Cálculo da umidade absoluta

O conteúdo de água real do ar, a umidade absoluta (a) [em gcm ^-3], resulta da umidade máxima (A) [em gcm^-3] e da umidade relativa do ar (U) [em%]:  

Os valores de estação assim calculados para a umidade absoluta são então regionalizados de acordo com o procedimento descrito acima e são depois convertidos em umidade relativa. A vantagem deste método de regionalização bastante complexo é que, para além da sua maior relação física, a umidade absoluta é mais dependente da altura do que a umidade relativa. Assim, o efeito de elevação pode ser utilizado para a regionalização de acordo com o procedimento descrito acima. Após a regionalização da umidade absoluta, a conversão em umidade relativa pode ser realizada. No entanto, em vez da temperatura da estação, a temperatura média do ar T_mean anteriormente regionalizada do subzona discreta correspondente é definida.