Da ILMS-Wiki

(Diferença entre edições)

Revisão das 20h35min de 26 de Fevereiro de 2013

Este tutorial descreve os processos importantes e algorítimos de diferentes módulos dentro do modelo hidrológico J2000 em detalhes:

Índice

1 Módulo de distribuição de precipitação
2 Módulo de interceptação
3 Módulo de neve
4 Módulo de geleira
5 Módulo de água do solo
6 Groundwater module
7 Routing module

Módulo de distribuição de precipitação

Parâmetros de calibração

Parâmetro	Descrição	Variação global	Para o modelo Dudh Kosi
Trans	temperatura limiar	0 + 5	2
Trs	temperatura base para a neve e chuva	-5 +5	0

No sistema de modelagem J2000, a precipitação é primeiramente distribuída entre chuva e neve, dependendo da temperatura do ar. Dois parâmetros de calibração (trans e trs) são utilizados, sendo que trs é a temperatura base e trans é uma gama de temperatura (limite superior e inferior), acima e abaixo da temperatura base. A fim de determinar a quantidade de neve e chuva, presume-se que a precipitação abaixo de certas temperaturas limite resulta em precipitação totalmente de neve e acima de um segundo limite em precipitação totalmente em estado líquido. No intervalo (trans) entre as referidas temperaturas limite, a precipitação ocorre em forma mista. Entre esses limites, misturas de chuva e neve com percentuais variáveis para cada componente são calculadas. A quantidade de neve real (P (s)) da precipitação diária sujeita à temperatura do ar é calculada de acordo com:

$Ps = \frac{TRS + Trans - T}{2 \cdot Trans} \, \, \, \mathrm{[mm]}$

A quantidade diária de neve (P_s) ou a quantidade de chuva (P_r)são calculadas de acordo com:

$Ps = Precipitation \cdot Ps \,\,\, \mathrm{[mm]}$

$Pr = Precipitation \cdot (1- Ps) \,\,\, \mathrm{[mm]}$

Estes parâmetros são considerados como parâmetros não-flexíveis e não são necessariamente colocados no âmbito do JAMS como parâmetros ajustáveis.

Relevâncias na modelagem

Configurar os valores trs abaixo de zero (por exemplo, 2) vai trazer mais precipitação sob a forma de "chuva" do que de "neve".

Módulo de interceptação

A interceptação é um processo durante o qual a precipitação é armazenada em folhas e outras superfícies abertas da vegetação. Durante a precipitação, ocorre a interceptação pelo dossel da plantas e de camada de resíduos. Este processo é identificado como componente importante de um ciclo hidrológico que pode afetar os componentes do balanço hídrico. A interceptação de copas e de resíduos é considerada uma perda para o sistema, já que qualquer chuva interceptada por qualquer um destes componentes subsequentemente evaporará (Kozak et al. 2007). O módulo de interceptação no sistema de modelagem J2000 serve como cálculo do volume de precipitação a partir da precipitação observada no contexto das coberturas vegetais particulares e do seu desenvolvimento no ciclo anual. A precipitação observada é reduzida pela parte interceptada para calcular-se o volume de precipitação. Assim a precipitação líquida apenas ocorre quando a capacidade máxima de armazenamento de interceptação da vegetação é atingida. O excedente é então repassado como precipitação interceptada para o próximo módulo. O módulo de interceptação utiliza uma abordagem simples de armazenamento de acordo com Dickinson (1984), que calcula a capacidade máxima de armazenamento de interceptação com base no Índice de Área Foliar (LAI), do tipo específico de cobertura do solo. O esvaziamento do armazenamento de interceptação é feito exclusivamente por evapotranspiração. A capacidade máxima de interceptação (Int_max) é calculada de acordo com a seguinte fórmula:

$Int_{max} = \alpha \cdot{LAI} \, \, \, \mathrm{[mm]}$

com

α ... capacidade de armazenamento por m² de área foliar em relação ao tipo de precipitação [mm]

LAI ... LAI da classe de uso da terra especial previsto no arquivo de parâmetros do uso da terra [-]

O parâmetro “a” tem um valor diferente, dependendo do tipo da precipitação interceptada (chuva ou neve), visto que a capacidade máxima de interceptação da neve é sensivelmente mais elevada do que a precipitação em estado líquido. O LAI para os tipos de vegetação individuais é fornecido no arquivo de parâmetros de uso da terra ao longo do ano. Porque o LAI muda de acordo com as estações do ano, quatro tipos diferentes de LAI para quatro estações diferentes para cada tipo de vegetação são propostas no arquivo de parâmetro do uso da terra. O valor do LAI pode ser determinado por medição direta de folhas, literatura e conhecimento especializado.

Módulo de neve

Parâmetros de calibração

Parâmetro	Descrição	Variação global	Para modelo Dudh Kosi
snowCritDens	Densidade crítica de neve	0 to 1	0.381
snowColdContent	conteúdo de frio do bloco de neve	0 to 1	0.0012
baseTemp	temperatura de limite para fusão da neve	-5 to 5	0
t_factor	fator de fusão pelo calor sensível	0 to 5	2.84
r_factor	fator de fusão pela precipitação líquida	0 to 5	0.21
g_factor	fator de fusão em pelo pelo fluxo de calor no solo	0 to 5	3.73

Estes parâmetros são fornecidos em negrito e itálico na descrição abaixo:

O módulo de neve calcula as diferentes fases de acumulação de neve, metamorfose e neve derretida. O módulo mais complexo é adaptado no modelo de Knauf (1980). O módulo de neve leva em conta as mudanças de estado do bloco de neve durante a sua existência, especialmente suas mudanças de densidade devido ao degelo e a subsidência. Este processo é importante porque o bloco de neve pode armazenar água livre, como uma esponja, até atingir uma densidade de certo limite e só então uma descarga súbita de água ocorre. Para o modelo, capacidades diferentes de água da camada de neve são considerados: o equivalente real da água da neve (SWEdry) que corresponde à quantidade de água que realmente congelou e o equivalente total de água da neve (SWEtotal) que, além disso, considera a água em estado líquido armazenada no bloco de neve. A subsidência do bloco da neve, que resulta da água líquida através da fusão à superfície ou a partir da precipitação de chuva, é calculada de acordo com subsidência empírica (esquema de compactação da neve) por Bertle (1966).

A camada de neve e as suas condições estão descritas no modelo de acordo com os seguintes parâmetros: profundidade da neve (SD) [mm], a densidade da neve seca (dryDens)} [em g/cm³] como o quociente do teor total de água e da profundidade da neve.

Se houver uma temperatura do ar mínima, média e máxima para um determinado período de tempo (dados diários), o módulo calcula a acumulação separada ou temperaturas de fusão. A acumulação e fusão pode ocorrer dentro de um intervalo de tempo. As temperaturas de fusão e de acumulação (T_acc e T_melt) podem ser calculadas de acordo com:

$T_{acc} = \frac{T_{min} + T_{avg}}{2} \,\,\,\,\,\,[^oC]$

$T_{melt} = \frac{T_{max} + T_{avg}}{2} \,\,\,\,\,\,[^oC]$

Fase de acumulação:

O módulo de neve simula a acumulação e a compactação da camada de neve causada pelo degelo ou chuva na precipitação de neve.

As circunstâncias térmicas sob a cobertura de neve são levadas em consideração juntamente com o teor de frio dessa cobertura em conexão com o degelo. Na temperatura abaixo do ponto de congelamento, o bloco de neve arrefece significativamente. Já que a água derretida congela imediatamente devido a circunstâncias isotérmicas negativas sob a cobertura de neve, não ocorre escoamento. O teor de frio tem de atingir o valor zero, de modo que o processo de degelo comece novamente. Consequentemente, as temperaturas negativas elevam o teor de frio enquanto que a temperatura positiva reduz-lo. O cálculo do armazenamento de conteúdo de frio resulta do produto da temperatura do ar por um parâmetro de calibração (coldContFact).

$CC = coldContFact \cdot T \,\,\,\,\,\,[mm]$

Ao fazê-lo, temperaturas negativas do ar são acumuladas e diminudídas apenas por temperaturas positivas e pelas potenciais taxas resultantes de fusão. Só quando o teor de frio tiver atingido um valor de 0, ocorre o derretimento da neve.

Se a temperatura do ar for inferior a -15 ° C, pressupõe-se que a densidade da neve nova seja 0,02875.

A mudança de profundidade da neve (SD δ) resultante da precipitação da neve é calculada de acordo com seguinte premissa: a acumulação de neve ocorre no modelo se a precipitação cair sob a forma sólida (NewsNow> 0). Portanto, a densidade de neve nova é determinada sujeita a temperatura do ar. O cálculo é realizado de acordo com (Kuchment 1983, e Vehvilaeinen 1992), se a temperatura do ar for superior a -15 oC.

$newSnowDens = 0.13 + 0.0135 \cdot T_{acc} + 0.000045 \cdot T^{2}_{acc}\,\,\,\, [g/cm^3]$

Se a temperatura do ar for inferior a -15 ° C, pressupõe-se que a densidade da neve nova seja 0,02875.

A mudança de profundidade da neve (SD δ) resultante de sua precipitação e é calculada da seguinte forma:

$δ SD = \frac{netSnow}{newSnowDens} \,\,\,\,\,\,[mm]$

O equivalente de água da neve do dia anterior (\textit{SWEdry}) aumenta o valor de precipitação de neve de acordo com:

$SWEdry_{{t}} = SWEdry_{{t-1}} + netSnow \,\,\,\,\,\,[mm]$

O equivalente de água da neve seca e o equivalente total de água da neve são aumentados pelo mesmo valor. Se o evento de precipitação envolvido precipitação mista (chuva/neve), a quantidade de chuva é atribuída ao equivalente total de água da neve.

Se a chuva é parte do evento de precipitação, ocorre como resultado a subsidência do bloco de neve. O cálculo da quantidade de subsidência é discutido abaixo. No modelo, o bloco de neve permanece em fase de acumulação até que o valor de temperatura (T_melt) para o degelo exceda um valor limite (baseTemp), que tem de ser determinado durante a fase de parametrização da aplicação da modelagem. Em seguida, ele entra na fase de metamorfose que simula os processos de fusão e subsidência. No entanto, ele pode voltar para a fase de acumulação, se as temperaturas forem correspondentemente baixas. Devido aos valores de temperatura diferentes, os processos de acumulação e de fusão podem ser modelados durante um único intervalo de tempo.

Fase de fusão e subsidência:

Se o valor da temperatura de fusão (T_melt) exceder o valor limite da temperatura (baseTemp), , o bloco de neve passa da fase de acumulação para a de metamorfose. A quantidade de energia que é necessária para a fusão da neve está disponível em três formas diferentes. Em primeiro lugar, através de uma entrada de calor sensível por temperatura do ar (t_factor), em segundo, por precipitação a partir de uma fonte de energia na forma de chuva (r_factor) e em terceiro, pela entrada devido a um fluxo de calor no solo (g_factor). A soma de todas as entradas de energia fornece a taxa potencial de degelo (Mp). O cálculo da Mp é realizado de acordo com:

$Mp = t\_factor \cdot T_{melt} + r\_{factor} \cdot netRain \cdot T_{melt} + g\_{factor} \,\,\,\,\,\,[mm]$

A Mp variável é, então, também modificada de acordo com a inclinação e da exposição da unidade de modelo espacial (ou seja a HRU):

$Mp = \ Mp \cdot actSlAsCf \,\,\,\,\,\,[mm]$

A Mp é inicialmente usada para equilibrar o teor de frio da cobertura de neve e, em seguida, é também utilizada para gerar o derretimento da neve. A taxa de degelo potencial seguida é tomada para calcular-se a variação máxima resultante da profundidade da neve (SD δ):

$δ SD = \frac{M_P}{dryDens} \,\,\,\,\,\,[mm]$

Se δ SD for maior do que a profundidade da neve inteira, ela descongela completamente e o equivalente de água total da neve contribui para a geração de escoamento em forma de degelo. Se este não for o caso, a profundidade da neve é reduzida de forma correspondente, o que não altera o equivalente de água de neve no início. Em vez disso, o resultado é um aumento na densidade total da cobertura da neve.

Além dessa mudança na densidade, as alterações adicionais na subsidência e densidade de acordo com o esquema de compactação de neve (Bertle 1966) são levados em conta. Este método baseia-se no fato de que a água, não importando se ela resulta de temperatura induzida por degelo ou de precipitação, se infiltra na camada de neve, o que leva à subsidência por recristalização da neve e por alterações estruturais e de concentração no armazenamento (Knauf 1980). A taxa de subsidência resultante é calculada usando o método para a subsidência de neve descrita por Bertle (1966). Este método baseia-se na observação de uma relação empírica entre o influxo de água livre e a alteração resultante na elevação por subsidência, que foi derivado a partir de experiências de laboratório do Bureau of Reclamation EUA. Para o cálculo, o aumento do conteúdo de água acumulada em percentagem é visto em relação ao equivalente de água de neve usando a seguinte fórmula:

$P_w = \frac{totSWE}{drySWE} \cdot 100 \,\,\,[\%]$

Esta equação mostra que quanto mais água em estado líquido houver como entrada, maior será a subsidência do bloco de neve (P\_w) (Knauf 1980). Uma entrada da quantidade exata de água correspondente ao equivalente da água da neve do bloco leva a uma redução para a metade da profundidade da neve por subsidência. A percentagem da mudança da profundidade da neve (P$_H$) é calculada sujeita à entrada de água livre:

$P_H = 147.4 - 0.474 \cdot P_W \,\,\,[\%]$

A nova profundidade de neve (SD) é:

$SD = SD \cdot \frac{P_H}{100} \,\,\,[mm]$

Juntamente com a profundidade da neve que foi calculada, a densidade total \textit{(totDens)} e a densidade da neve seca \textit{(dryDens)} são calculadas de acordo com as seguintes fórmulas:

$dryDens = \frac{SWE_{dry}}{SH} \,\,\,[g/cm^3]$

$totDens = \frac{SWE_{tot}}{SH} \,\,\,[g/cm^3]$

Escoamento proveniente de derretimento

A camada de neve pode armazenar a água em estado líquido nos seus poros até uma certa densidade crítica (snowCritDens). Esta capacidade de armazenamento é perdida quase que completa e irreversivelmente quando uma certa quantidade de água em estado líquido em relação à SWE total (entre 40 e 45%) é atingida de acordo com Bertle (1966), Herrmann (1976) e Lang (2005). Neste limite, a capacidade de retenção de um bloco de neve que esteja naturalmente se desenvolvendo também é subitamente diminuída sem o impacto da chuva. Em tal caso, uma liberação súbita de água a partir do bloco de neve podem ser observada (Herrmann, 1976). No modelo, este processo é simulado através do cálculo de um teor máximo de água da cobertura de neve (SWE_max) de acordo com:

$WS_{max} = snowCritDens \cdot SD \,\,\,\,\,\,[mm]$

A densidade crítica (snowCritDens) precisa de ser fornecida pelo utilizador do modelo. A água armazenada no bloco de neve que exceder esse limite é transmitida como escoamento de neve (Q_snow).

$Q_{snow} = SWE_{tot} - SWE_{max} \,\,\,\,\,\,[mm]$

Nos intervalos de tempo seguintes, a densidade da camada de neve mantém a densidade limiar crítica, até que a mesma seja descongelada ou inicie a acumulação devido à queda de neve recorrente.

Módulo de geleira

O módulo de geleira foi desenvolvido e adaptado como uma parte da pesquisa de doutorado (Nepal, 2012) realizado sobre a bacia hidrográfica do Kosi Dudh. As informações fornecidas aqui são tomadas a partir deste estudo.

O módulo geleira está integrado no modelo hidrológico J2000 padrão, como parte desse estudo. Ele é tratado como um módulo separado dentro do J2000 em que o escoamento do degelo tanto da neve quanto do gelo (SIM) é calculada e resultado é passado diretamente a um rio como escoamento superficial (RD1). A abordagem sugerida por Hock (1999) foi implementada no modelo J2000 e ainda adaptada para a o cálculo do degelo. Esta abordagem considera o degelo utilizando um fator de dia-grau. A partir deste estudo, a inclinação, o aspecto e o fator de coberturas de detritos são ainda incluídos no modelo para o escoamento de degelo. O derretimento da neve na área glacial é calculada da mesma maneira como descrito anteriormente. O fluxo de calor do mesmo solo (parâmetro de calibração: g_factor) é proposto para o degelo nas zonas glaciais, já que a maioria das geleiras ficam cobertas por detritos e se comportam semelhante ao solo.

A área de geleira é fornecida como uma camada GIS que fornece uma ID exclusiva do uso da terra para as geleiras durante a delimitação da HRU. Todos os processos que ocorrem na geleira são tratados separadamente com base nessa identificação única. Primeiro a neve sazonal ocorre no topo da geleira (ou HRU de geleira). O modelo primeiro trata a neve, tal como descrito no “módulo de neve”, e produz o seu escoamento. A fim de se certificar de que o degelo ocorre, duas condições têm de ser preenchidas. Primeiro, a cobertura de neve inteira de uma HRU de geleira tem que derreter (ou seja o armazenamento deve ser zero). Em segundo lugar, a temperatura de base (tbase), tal como definida pelos utilizadores, tem de ser inferior a meltTemp. Só nestas condições, o material fundido de gelo ocorre como um progresso de modelo.

$meltTemp = \frac {Tmax + Tmean} {2} \,\,\,\,\,\,[^oC]$

A taxa de fusão para gelo glacial (iceMelt)(mm/dia) é obtido através da seguinte equação:

$iceMelt = \frac{1}{n} \cdot meltFactorIce + alphaIce \cdot radiation \cdot (meltTemp - tbase) \,\,\,\,\,\,[mm]$

sendo que:

radiation = radiação real global

meltFactIce = fator de derretimento generalizado de gelo como um parâmetro de calibração

alphaIce = coeficiente de derretimento para o gelo

n = intervalo de tempo (isto é, para o modelo diário, n = 1)

A fusão do gelo é ainda adaptada ao fator coberto de detritos. Já que as geleiras na bacia do rio Kosi Dudh estão cobertas por detritos em geral, um método simples de segregação é aplicado para identificar os restos cobertos de geleiras, com base no declive. Se a inclinação for superior a 30 graus, cascalhos, pedras e seixos rolam com gravidade e a geleira é considerada limpa. Uma inclinação inferior a este limiar é adequada para a acumulação de detritos nos topos da geleiras. Usando essa abordagem, cerca de 77% das geleiras são estimadas como geleiras cobertas por restos. De acordo com Mool (2001a), cerca de 70% das geleiras na bacia do rio Kosi Dudh são tipos de vale. Uma das características mais comuns de geleiras localizadas na região do Himalaia é a presença de detritos. Em geral, geleiras de vale são cobertas por resídos na região do Himalaia (Fujji 1977;. Sakai2000). Pode-se supor que as áreas de geleiras cobertas por detritos, que são estimadas por esta abordagem, são bastante representativas e adequadas para os fins deste aplicativo de modelagem.

A presença de detritos afecta o processo de ablação. Uma cobertura supra-glacial de detritos, com espessura superior a alguns centímetros, leva a uma redução considerável na taxa de fusão (Oestrem 1959; e Mattson, 1993). De acordo com Oestrem (ibid.) a taxa de fusão diminui quando a espessura da cobertura de detritos for maior do que cerca 0,5 cm. O relatório ainda menciona que, não só a fusão será mais lenta sob a camada de moreia, mas também o período de ablação será mais curto para o gelo coberto. As geleiras limpas como relatado no planalto tibetano têm taxas mais altas de recuo. Kayastha (2000) estudou o padrão de degelo das geleiras do Khumbu (na bacia do Dudh Kosi onde o modelo J2000 está sendo aplicado) e descobriu que os detritos com espessura de 0 a 5 cm indica que a ablação do gelo é aumentada até um máximo de 0,3 cm. Portanto, quando uma geleira é coberta por detritos, o degelo é reduzido. Usando o parâmetro de calibração (debrisFactor), os efeitos da cobertura de detritos sobre a fusão são controlados da seguinte maneira.

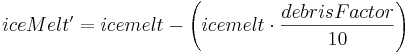
$iceMelt' = icemelt - \left(icemelt \cdot \frac{debrisFactor}{10}\right)$

O degelo é mais adaptado à inclinação e ao aspecto do HRU de geleira em particular. O roteamento da fusão glacial é feito separadamente para o degelo e o escoamento da chuva através da seguinte fórmula:

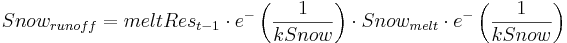
$Snow_{runoff} = meltRes_{t-1} \cdot e^ -\left(\frac {1}{kSnow}\right) \cdot Snow_{melt} \cdot e^ -\left(\frac {1}{kSnow}\right)$

sendo que:

snow_melt = derretimento total da neve durante o intervalo de tempo (mm/dia)

meltRes_t-1 = saída do reservatório durante o intervalo de tempo anterior

kSnow = coeficiente de armazenamento (constante de recessão) para reservatório

Um procedimento de roteamento semelhante é aplicado para o escoamento do degelo e da chuva com uma constante de recessão diferente (kIce) e (kRain). Presume-se que o roteamento do escoamento da chuva é mais rápido do que o de gelo e neve.

Na verdade, a neve é armazenada na zona de acumulação de zonas de altitude elevada. Ela é então transportada para a baixa altitude pelo vento, por avalanches e pela gravidade. Como ela é enterrada sob a neve nova, a neve é gradualmente convertida em uma massa firme e eventualmente em gelo glacial. Este gelo flui rio abaixo através da ação da gravidade para a zona de ablação como geleiras (Jansson, 2003). No entanto, tais processos dinâmicos de transformaçãoe do transporte da neve não estão incluídas no módulo de geleira do modelo J2000. Portanto, uma parte da precipitação é sempre armazenada em forma de neve na zona de acumulação de áreas de alta altitude. Para compensar este processo de armazenamento de longo prazo, uma camada de geleira constante é utilizada como um substituto que proporciona a fusão do gelo glacial.

Módulo de água do solo

A descrição do módulo de água do solo, conforme descrito no modelo de código fonte está disponível nessa seção, a qual é principalmente baseada na documentação técnica do modelo J2000 (Krause, 2011).

No módulo de solo, solos separados são representados de acordo com os seus volumes de poros. O armazenamento de poros, que pode ocorrer no solo, é classificado na literatura como se segue (por exemplo, (Scheffer & Schachtschabel 1984)):

A água armazenada em poros finos (< 0.2 μm de diâmetro, PF> 4.2, corresponde ao ponto de emurchecimento permanente - PWP) fica tão fortemente ligada devido aos poderes de absorção desses, que ela não gera escoamento.

A água armazenada em poros médios (diâmetro de 0,2 a 50 μm, pF 1,8 a 4,2, corresponde à capacidade de campo utilizável - nFk) fica suspensa contra a gravidade devido ao seu poder de absorção. Ela pode ser extraída do solo, quase que exclusivamente por meio do potencial de sucção.

A água armazenada nos poros grossos e macro (> 50 μm de diâmetro, pF> 1,8, corresponde à capacidade do ar - Lk) fica sujeita à gravidade e pode ser mantida no solo durante apenas um curto período de tempo (1-2 dias de acordo com (Scheffer & Schachtschabel 1984).

A água armazenada nos poros finos pode ser negligenciada durante a modelagem, já que ela não está disponível para os processos de evaporação ou de fluxo de acordo com a especificação acima mencionada dos volumes dos poros, devido à constante de ligação. Por isso, a abstração de modelagem do solo é realizada por dois armazenamentos paralelos e ligados no modelo J2000: um armazenamento que corresponde ao volume do reservatório de poros médios (a partir deste ponto referido como MPS – Middle Pore Storage) e que só pode ser esvaziado por meio de evaporação e outro reservatório que representa o volume do reservatório de poros grandes e macro (daqui em diante referido como LPS – Large Pore Storage) e que é a fonte para o escoamento efetivo.

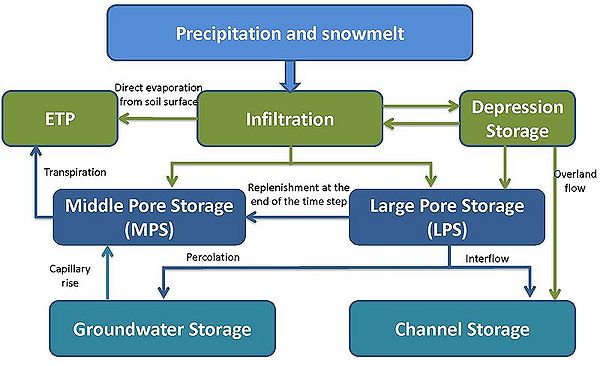
A figura abaixo mostra os processos hidrológicos importantes dentro da zona do solo. Pode-se ver que um armazenamento de infiltração precede o do solo, o qual contém água e precipitação líquida resultante da fusão da neve. A partir desse, a água é distribuída para os reservatórios do solo, onde a água restante é armazenada no reservatório de depressão, caso ela exceda a capacidade máxima de infiltração do solo correspondente, ou uma saturação do armazenamento de poros grandes ocorra. O esvaziamento desse reservatório de depressão é feito por meio de evaporação, geração de escoamento superficial e/ou infiltração num ponto posterior no tempo. Já o esvaziamento do reservatório de poros médios é feito por evapotranspiração, esvaziando o reservatório de poros grandes, gerando interfluxo ou por recarga. Além disso, no final do intervalo de tempo, uma determinada quantidade de água armazenada no LPS pode ser transferida para o reservatório de poros médios. Esse último pode, adicionalmente a esta quantidade de água e à infiltração, receber a água da zona saturada, devido à subida capilar. Estes processos individuais são explicados em detalhe a seguir (a parametrização do módulo de solo já foi demonstrada).

Infiltração

O primeiro processo, que contém a água resultante da fusão da neve e do volume de precipitação é a infiltração. Se a água pode se infiltrar inteiramente ou se ela é armazenada por um curto período de tempo na superfície e se ela gera um reservatório de depressão nesse lugar ou um escoamento superficial, depende da capacidade de infiltração do solo correspondente. Essa capacidade é calculada através de um método simplificado que é adequado para os intervalos de tempo diários. Ela se baseia no pressuposto de que a capacidade de infiltração é por um lado sujeita a saturação de água no solo e, por outro, não pode exceder um certo limite, a uma taxa de infiltração máxima. Se esta taxa de infiltração máxima for definida para um valor constante médio para todo o ano, haverá dois problemas, pelo menos para dois casos especiais:

Na precipitação convectiva com altas intensidades e curta duração. Muitas vezes, a capacidade de infiltração do solo é ultrapassada, uma vez que muita água chega ao solo dentro de um curto período de tempo, embora a quantidade de precipitação durante o dia todo não implique nisso.

No escoamento do derretimento da neve da cobertura de neve. Embora a água seja liberada de uma maneira bastante contínua, o solo se comporta como uma área vedada, uma vez que está, em parte ou totalmente congelado, ou já que a água escorre dentro da cobertura de neve sem sequer ter a chance de se infiltrar.

A fim de ter esses casos especiais em conta, pelo menos rudimentarmente, dois valores limite podem ser indicados além do "valor padrão". Dado que o primeiro caso especial ocorre principalmente nos meses de verão, um valor limite pode ser especificado para a metade do ano de verão. Este valor serve para levar em conta tempestades com alta intensidade dentro de um curto período de tempo, que ocorrem principalmente durante os meses de verão. O segundo valor limite é aplicado se a unidade modelada estiver coberta de neve. Utilizando este valor reduzido, é considerada a capacidade de infiltração do solo, com uma superfície total ou parcialmente congelada. Ao mesmo tempo, este valor pode ser usado para se levar em consideração o escoamento da água resultante do degelo e da precipitação dentro da cobertura de neve. O terceiro valor representa o caso padrão e, portanto, é válido para a medate do ano de inverno e para entidades sem cobertura de neve.

Os valores limite, que devem ser determinados pelo usuário (soilMaxInfSummer, soilMaxInfSnow, soilMaxInfWinter referidos abaixo na equação como soilMaxInf1,2,3) são ponderados durante a modelagem com o déficit de saturação relativa do solo (δ_sat). A taxa de infiltração máxima resultante ( Inf_max), é em seguida calculada de acordo com:

$Inf_{max} = soilMaxInf_{1, 2, 3} \cdot (1 - satSoil) \,\,\, [mm/d]$

A saturação de água do solo relativa pode ser calculada usando:

$soilSat = \frac{actMPS + actLPS}{maxMPS + maxLPS} \,\,\, [mm/d]$

Se a quantidade de água da precipitação e do derretimento da neve para a infiltração exceder a taxa de infiltração máxima calculada, o excesso é transferido para o reservatório de depressão, onde fica armazenando. A resultante quantidade de água que escoa de fato (Inf_act ) é distribuída entre os reservatórios do solo. A quantidade de água que se encontra em cada desses fica sujeita ao deficit de saturação do reservatório de poros médios (MPS) e é calculado usando os parâmetros de calibraçãosoilDistMPSLPS como se segue:

O reservatório de poros médios (MPS) recebe a água restante de acordo com:

$MPS_{in} = Inf_{act} \cdot \frac{1 \cdot soilDistMPSLPS}{satMPS} \,\,\, [mm]$

O reservatório de poros grandes (LPS) recebe a água restante de acordo com:

$LPS_{in} = Inf_{act}-MPS_{in} \,\,\, [mm]$

Devido à distribuição de água de acordo com essas equações, o reservatório de poros médios funciona como uma esponja e o seu potencial de absorção de água aumenta com a crescente desidratação. No entanto, uma certa quantidade sempre permanece no LPS. A distribuição ponderada tem a vantagem de que, mesmo em solos secos, especialmente durante os meses de verão, parte da água infiltrada pode escorrer rapidamente. Se a água não foi distribuída, o interfluxo só poderá ocorrer após a saturação do MPS, ou seja, após atingir a capacidade de campo utilizável. Várias investigações demonstraram que os poros grandes e macro também podem alcançar o escoamento se não houver saturação de água no solo.

Outros casos especiais de infiltração ocorrem com áreas seladas e áreas aquáticas. Para áreas aquáticas, a água que está realmente disponível para a infiltração é transferida para um armazenamento individual, que pode apenas ser esvaziado por meio de evaporação. Em áreas seladas apenas uma certa quantidade de água sobre a superfície escorre, sujeita ao grau de vedação (por exemplo, 25% com um grau de vedação > 80%, e 60% com um grau de vedação < 80% de acordo com (Wessolek 1993). A parte restante contribui para o escoamento total, na forma de escoamento superficial. Isto é considerado usando coeficientes correspondentes (soilImpGT80, soilImpLT80) que têm que ser ajustadas pelo usuário.

O reservatório de depressão

Como representado na descrição da infiltração acima, a quantidade de água que excede a velocidade de infiltração máxima do solo é transferida para o reservatório de depressão. Isto também se aplica se o solo estiver completamente saturado com água e infiltração alguma puder ocorrer. A água, que é armazenada no reservatório de depressão corre em parte como escoamento superficial. A quantidade máxima em mm m {-2}, que pode ser mantida como reservatório de depressão indivídual, tem de ser indicada durante parametrização do modelo. De acordo com Maniak (1997), o reservatório de depressão máximo situa-se entre 0,6 e 8,0 mm por m², estando sujeito ao uso do solo específico. Uma vez que esta variável tem um impacto relativamente baixo sobre a dinâmica das linhas de escoamento (ibid.), o reservatório de depressão máximo é definido com um valor fixo e não é diferenciado de acordo com o uso da terra. À medida que esse reservatório é apenas importante em locais de baixa elevação, o reservatório de depressão máximo é ponderado utilizando a inclinação da área específica. Como, também de acordo com Maniak (1997), esse reservatório máximo diminui em 50% a partir de um declive de 4-6%, o seu volume é reduzido à metade para as zonas superiores a esta inclinação. Se o reservatório de depressão máximo for superior a uma área, o excesso de água é lançado como escoamento superficial.

O reservatório de poros médios

A água armazenada nos poros médios do solo é mantida contra a gravidade, devido às forças de absorção. Isto significa que um potencial ativo de água do solo é requerido de modo a extrair a água desse armazenamento. O potencial para a sucção de água do solo é disponibilizado por meio da evaporação. Dois casos diferentes têm de ser distinguidos: a evaporação direta da superfície do solo e da evaporação causada pela transpiração da cobertura vegetal. A evaporação direta da superfície do solo é comparativamente baixa, uma vez que apenas alguns milímetros de solo seco podem causar um isolamento eficaz das camadas subjacentes em relação à evaporação. Este isolamento é encurtado pelas raízes da vegetação que possibilitam uma consistente exaustão por transpiração da água armazenada nos poros médios. Com o aumento da desidratação do solo, a evaporação efetiva diminui significativamente em relação ao potencial de evaporação. Para simular esta redução, é utilizada uma abordagem linear estabelecida ([Gurtz et al 1997.]; [Schulla 1997]; [Uhlenbrook 1999]) ou é aplicada uma abordagem não linear que tenha sido desenvolvida para o modelo.

Quando se utiliza a abordagem linear, pressupõe-se que a evaporação seja igual ao verdadeiro potencial de evaporação até que uma saturação de água específica seja atingida. Quando o valor for inferior a esta saturação de água, a evaporação real diminui de forma consistente em relação à evaporação, até que o potencial seja zero, quando se atinge o ponto de muchamento permanente (= esvaziamento completo da nFk). Como o valor limite (soilLinRed) para esta saturação de água específica, valores entre 0,8 - 0,6 são mencionados na literatura ([Gurtz et al 1997.]; [Menzel 1997]). Este valor limite e a saturação de água real do reservatório de poros médios M (satMPS) é usado para calcular o fator de redução (RF):

$RF = 1 for satMPS \geq soilLinRed$

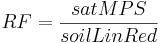
$RF = \frac{satMPS}{soilLinRed}$

O reservatório de poros grandes

A água que se encontra no reservatório de poros grandes (GPS) está sujeita à gravidade e é, portanto, considerada como a fonte de processos de fluxo efetivos e da geração de escoamento do solo em J2000. O enchimento desse reservatório é feito pela quantidade de infiltração que permanece depois de subtrair-se o influxo para o reservatório de poros médios.

O comportamento de escoamento diferente dos diferentes solos é refletido muito bem pelos volumes de poros que foram definidos previamente. O solo argiloso tem uma proporção relativamente elevada de poros finos e médios, enquanto que o solo arenoso tem um valor comparativamente elevado de poros grandes. A geração de escoamento lateral e vertical e da quantidade de precipitação é correspondentemente diferente. A água, que é armazenada no solo argiloso, contribui menos para o escoamento lateral e vertical sob as mesmas condições (por exemplo, cobertura de vegetação, inclinação, etc), do que a do solo arenoso. Em contraste, a quantidade de água disponível para a evaporação é significativamente mais elevada em solos argilosos do que em solos arenosos. O solo argiloso ou lodoso, que se situa entre os solos acima mencionados de acordo com o seu tamanho de poro, possui a melhor capacidade de armazenamento de água, uma vez que ele tem a maior quantidade de poros médios.

A quantidade de água que gera o escoamento a partir do reservatório de poros grandes no intervalo de tempo fica sujeita à saturação de água relativa do solo inteiro (LPS_soil) e é calculada de acordo com:

$Q_{LPS} = (Sat_{soil})^\alpha\ \cdot LPS_{act} \,\,\, [mm]$

sendo que:

Q_LPS: fluxo de saída do LPS [mm]

Sat_soil: saturação de água relativa do solo no local [-]

α : coeficiente de calibração [-]

A vantagem desta função de escoamento não linear é que muito menos água escorre em baixa humidade areal do que a de uma função de drenagem linear. O comportamento comum das zonas de captação que geram um escoamento muito maior e mais rápido quando há uma elevada humidade do solo (Baumgartner & Liebscher 1990; Dyck & Peschke 1995) do que quando há baixa humidade (presumindo a mesma quantidade de precipitação) pode ser exibido usando uma melhor função de escoamento.

A água de gravitação que flui para fora do LPS (Q_LPS ) é distribuída entre três reservatórios de destino diferentes. Uma certa quantidade vai para o de poros médios e é armazenada aí durante um longo período de tempo, a segunda parte se infiltra no reservatório de água subterrânea (componente vertical) e a quantidade restante é a fonte para o interfluxo (componente lateral). O tamanho dos componentes está sujeito a parâmetros físicos do solo (especialmente valores kf) e a inclinação da HRU correspondente. Portanto, assume-se no modelo que a área de declive gera muito interfluxo, ao passo que em locais situados quase que interamente em planos, a percolação nas águas subterrâneas é o componente principal. A quantidade que vai de poros grandes a poros médios está, no entanto, sujeita à saturação do reservatório de poros médios. A fim de determinar os montantes de escoamento o declive e dois valores kf têm de ser especificados para cada HRU: O valor kf do horizonte do solo com a menor permeabilidade e o mesmo valor do horizonte sobrejacente.

Percolação e geração de interfluxo

Uma certa quantidade de água de gravitação disponível se infiltra no solo inteiro e contribui para a recarga das águas subterrâneas. Na apresentação de modelo do J2000 esta quantidade percolada é representada como dependente da inclinação da HRU correspondente. A inclinação influencia a percolação na medida em que as áreas inclinadas têm uma maior quantidade de água de gravitação como escoamento lateral de zonas não saturadas, ou seja, a recarga é menor nessas áreas do que em locais situados em planos. A influência da inclinação é levada em consideração, com um gradiente de acordo com a seguinte equação:

$grad_{perc} = (1 - tan \alpha)^\beta\ \,\,\, [-]$

α: inclinação da HRU correspondente [graus]

β: parâmetro de forma, coeficiente de calibração [-]

Ao usar-se esta equação da relação entre o escoamento vertical e lateral, determina-se o que pode ser adaptado para as condições na área de captação, com a ajuda do coeficiente de calibração β. Além disso, com este coeficiente de calibração pode ser melhorada a inclinação resultante de modelos de granulação grossa que é sistematicamente muito baixa.

A quantidade de água disponível para a percolação é calculada de acordo com:

$Perc_{pot}= grad_{perc} \cdot Q_{LPS} \,\,\, [mm]$

Esta taxa de percolação é então definida levando em consideração o coeficiente de calibração soilMaxPerc que descreve a taxa de percolação máxima por intervalo de tempo.

E para o Interfluxo (RD2):

$Interflow = 1- grad_{perc} \cdot Q_{LPS} \,\,\, [mm]$

A retenção de escoamento

Ambos os componentes de escoamento, de escoamento direto (RD1) e interfluxo (RD2) estão atrasados no tempo, com o objetivo de se considerar a expansão da área da unidade espacial do modelo. A retenção ocorre através de coeficientes de retenção correspondentes (soilConcRD1, soilConcRD2). Ela é calculado de acordo com:

$RD1 = \frac{1}{soilConcRD1} \cdot RD1{gen} \,\,\, [mm]$

$RD2 = \frac{1}{soilConcRD2} \cdot RD2{gen} \,\,\, [mm]$

Nepal (2012) sugeriu que, no caso de RD1, o tempo de atraso pode ser diferente durante períodos de alto fluxo, devido ao comportamento não-linear de uma bacia. Beven (2001a) destacou que as respostas não-lineares existem principalmente devido a duas causas. A primeira é a condição antecedente, quando a relação entre a precipitação e o escoamento é geralmente considerada como sendo não-linear, porque quanto mais humidecida for a zona de captação antes de uma unidade de entrada (input) de precipitação, maior será o escoamento gerado. A segunda é a existência de uma não-linearidade também devido à mudança de velocidade com descarga. As velocidades de fluxo médias aumentam com o fluxo de superfície e com processos de fluxo abaixo dela. Velocidades de fluxo mais rápidas significam que o escoamento chegará a um ponto de medição no sistema de fluxo de canal mais rapidamente. No caso de ocorrência de precipitações extremadas (por exemplo, durante a estação de monções na área de estudo), que são responsáveis por picos de cheias elevadas, um alto grau de não-linearidade é observado. Durante esses eventos, o solo fica saturado com os acontecimentos iniciais de precipitação e um maior coeficiente de chuva-escoamento é provável após alguns períodos de chuva. Estas condições típicas foram levadas em conta, o que acabou na introdução de um novo parâmetro para o sistema de modelagem do J2000. O novo parâmetro (concRD1Flood) é usado pelo modelo quando o RD1_gen cruza um valor limite (RD1FloodThreshold) fornecido pelo usuário. O valor de (concRD1Flood) deve ser mais baixo do que concRD1 porque produz um fluxo de saída RD1 mais elevado.

$RD1_{flood} = \frac{1}{soilConcRD1Flood} \cdot RD1{gen} \,\,\, [mm]$

Difusão

No final do intervalo de tempo, um défice de um reservatório de poros médios (MPS), resultante da evaporação, é compensado pela água do reservatório de poros grandes (LPS). Esta difusão (diff) é levada a cabo utilizando o coeficiente de calibração soilDiffMPSLPS de acordo com:

$diff = actLPS \cdot (1-e\frac{-1\cdot diff }{satMPS}) \,\,\, [mm]$

For more information see also: [Baumgartner & Liebscher 1990], [Dyck & Peschke 1995], [Gurtz et al. 1997], [Maniak 1997], [Menzel 1997], [Scheffer & Schachtschabel 1984], [Schulla 1997], [Uhlenbrook 1999], [Wessolek 1993].

Groundwater module

The model structure of the groundwater module in J2000 allows the presentation of the groundwater runoff of all geological formations existing in the catchment area by considering their storage and runoff behavior. Those formations have to be parameterized separately. The geological units are subdivided into the upper groundwater storage (RG1) in the weathered loose material with high permeability and short retention time and the lower groundwater storage (RG2) in the matrix and in fissures and ravines of the bedrock with low permeability and long retention time. Correspondingly, two basic runoff components are generated, a fast one from the upper groundwater storage and a slow one from the lower groundwater storage. Filling the groundwater storage results from the vertical runoff component of the soil module (percolation), emptying can be done by the lateral underground runoff components and the capillary rise on the unsaturated zone. The parameterization of the groundwater storage is carried out using the maximum storage capacity of the upper (maxRG1) and the lower groundwater storage (maxRG2) as well as the retention coefficient for both storages, (kRG1) and (kRG2). The maximum storage capacity can be estimated by multiplying the part of the underground chamber with the thickness of the individual storages per m² standard area. Both parameters have to be defined for every geological unit separately and have to be saved in the corresponding parameter file. The following table shows an example of such a parameter file.

The first process to be calculated is the capillary rise. It is assumed that this action takes place in the slow groundwater storage RG2. The calculation is done using the actual storage amount actRG2, the humidity deficit (deltaSoilStor) or the relative saturation (satSoilStor) in the upper soil and the calibration parameter gwCapRise. Capillary rise is calculated if the current storage amount of the groundwater storage is higher than the soil humidity deficit and the calibration parameter gwCapRise is above zero. By putting it to zero the capillary rise can be prevented.

If capillary rise is calculated, first the rise rate inSoilStor is calculated:

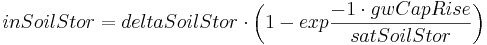
$inSoilStor = deltaSoilStor \cdot \left(1 - exp\frac{-1 \cdot gwCapRise}{satSoilStor} \right)$

It is then extracted from the groundwater storage RG2 and added to the upper soil water storage. After calculating the capillary rise the lateral inflow is considered. Hence, both inflow components inRG1 and inRG2 are added to the corresponding storages actRG1 and actRG2. If the maximum storage capacity is exceeded, surplus water is directly given to the runoff component.

The allocation of the percolation from the upper soil is carried out according to the slope of the specific model entity and a calibration coefficient (gwRG1RG2dist) in the following steps. First, the influence of the slope is considered:

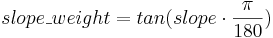
$slope\_weight = tan (slope \cdot \frac{\pi}{180} )$

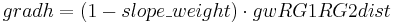
$gradh = (1 - slope\_weight) \cdot gwRG1RG2dist$

Then the percolation rate is allocated:

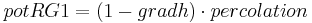
$potRG1 = (1-gradh) \cdot percolation$

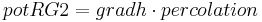
$potRG2 = gradh \cdot percolation$

The potential inflows are calibrated against the corresponding current storage. If RG2 cannot take the inflow pot_RG2 completely, the surplus is transferred to pot_RG1. If RG1 cannot take pot_RG1, the surplus is given to gwExcess. According to the model’s concept this variable can be assigned to a specific runoff component.

The calculation of water discharge is carried out according to the current storage amount in form of a linear storage-outflow function. The storage retention coefficients (kRG1, kRG2), which are considered as the time water rests in the specific storage, are a factor of the current storage volume (actRG1 and actRG2) used for the calculation of the groundwater outflow (outRG1 and outRG2) as follows:

$outRG1 = \frac{1}{gwRG1Fact \cdot kRG1} \cdot actRG1 \,\,\,[mm]$

$outRG2 = \frac{1}{gwRG2Fact \cdot kRG2} \cdot actRG2 \,\,\,[mm]$

The groundwater dynamics can be calibrated using parameters gwRG1Fact and gwRG2Fact.

Routing module

The J2000 module has two different routing components. The lateral routing component serves to simulate lateral flow processes in the catchment area until the water finally reaches a preflooder segment or a reservoir. In order to do so, the individual runoff components which are generated in the model entities are transferred to the corresponding recipient. This component does not have any calibration parameters.

The reach routing component is used for modeling flow processes in the on-site preflooder network of the catchment area. First, separate reaches have to be parameterized. The individual parameters which have to be assigned, are length in meters, slope in %, the mean width in meters and the reach roughness according to Manning-Strickler. Those are stored in a parameter file which is read by the model and by which the corresponding objects are generated. Additionally, the file contains information on the structure of the flow topology by noting the ID for every reach into which it empties. The reach representing the catchment outlet has to contain the ID 0.

The individual reaches receive water by neighboring spatial model entities and upstream reaches. In the reach, a velocity for water amount is calculated and then a certain amount is given to the next downstream reach based on the velocity and the length of the on-site preflooder. For the calculation a rectangular cross section is assumed to simplify matters. Although the complete amount of water is routed, the relative amounts of the individual runoff components are maintained, so they can be considered separately anytime and in every reach.

The module describes flow processes in the channel by using the kinematic wave approach and the calculation of velocity according to MANNING & STRICKLER. The only parameter that has to be set by the user (TA)(also referred as flowRouteTA) is a routing coefficient. It represents the runtime of the runoff wave which moves in the channel until it reaches the catchment outlet after a precipitation event. Its value is required for the calculation of the restraint coefficient (Rk) together with velocity of the river (v) and flow length (fl):

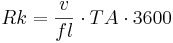
$Rk = \frac{v}{fl} \cdot TA \cdot 3600$

Before doing so, the velocity (v_new) has to be determined using the roughness factor by Manning (M), slope of the river bed (l) and the hydraulic radius (Rh). The hydraulic radius is calculated using the drained cross section (A) of the reach which results from the flow rate (q), velocity (v) and river bed width (b). For this approach, a start velocity (v_init) is assumed which is then iteratively adjusted with regard to the new calculated velocity (v_new) until both velocities differ in a value smaller than 0,001 m s^{-1}:

$Rh = \frac{A}{b + 2 \frac{A}{B}} \,\,\,\,[m]$

with: $A = \frac{q}{v_{init}} \,\,\,\,[m^2]$

$v_{new} = M \cdot Rh^{\frac{2}{3}} \cdot l^{\frac{1}{3}} \,\,\,\,[m^3/sec]$

$q = q_{act} \cdot e^{\frac{-1}{Rk}} \,\,\,\,[m^3/sec]$

Finally, the amount of water of the corresponding reach ( ) is calculated which goes to the runoff ( ) using the runoff restraint coefficient ( ) which has been generated.

$q = q_{act} \cdot e^{\frac{-1}{Rk}} \,\,\,\,[m^3/sec]$

The higher the assumed value of TA, the faster does the runoff wave move within a certain time span and the less water remains in the channel.

@@ Linha 313: / Linha 313: @@
-'''The large pore storage'''
+'''O reservatório de poros grandes'''
-The water which is in the large pore storage (GPS) is subject to gravitation and is therefore considered as the source of actual flow processes and runoff generation of the soil in J2000. Filling the storage is done by the infiltration amount which remains after subtracting the inflow to the middle pore storage.
+A água que se encontra no reservatório de poros grandes (GPS) está sujeita à gravidade e é, portanto, considerada como a fonte de processos de fluxo efetivos e da geração de escoamento do solo em J2000. O enchimento desse reservatório é feito pela quantidade de infiltração que permanece depois de subtrair-se o influxo para o reservatório de poros médios.
-The different runoff behavior of different soils is reflected very well by the pore volumes which have been defined beforehand. Clayey soil has a relatively high proportion of fine and middle pores, whereas sandy soil has a comparably high amount of large pores. The generation of lateral and vertical runoff and the amount of precipitation is correspondingly different. The water which is stored in rather clayey soil contributes less to lateral and vertical runoff, under the same conditions (e.g. vegetation cover, slope etc.), than does rather sandy soil. In contrast, the water amount available for evaporation is significantly higher in clayey soils than in sandy soils. Clayey or silty soil, which lies between the above-mentioned soils according to their pore size, has the best water storage capacities since it has the highest  amount of middle pores.
+O comportamento de escoamento diferente dos diferentes solos é refletido muito bem pelos volumes de poros que foram definidos previamente. O solo argiloso tem uma proporção relativamente elevada de poros finos e médios, enquanto que o solo arenoso tem um valor comparativamente elevado de poros grandes. A geração de escoamento lateral e vertical e da quantidade de precipitação é correspondentemente diferente. A água, que é armazenada no solo argiloso, contribui menos para o escoamento lateral e vertical sob as mesmas condições (por exemplo, cobertura de vegetação, inclinação, etc), do que a do solo arenoso. Em contraste, a quantidade de água disponível para a evaporação é significativamente mais elevada em solos argilosos do que em solos arenosos. O solo argiloso ou lodoso, que se situa entre os solos acima mencionados de acordo com o seu tamanho de poro, possui a melhor capacidade de armazenamento de água, uma vez que ele tem a maior quantidade de poros médios.
-The water amount which generates runoff from the large pore storage in the time step is subject to the relative water saturation of the entire soil (LPS<sub>soil</sub>) and is calculated according to:
+A quantidade de água que gera o escoamento a partir do reservatório de poros grandes no intervalo de tempo fica sujeita à saturação de água relativa do solo inteiro (LPS<sub>soil</sub>) e é calculada de acordo com:
 <math> Q_{LPS} = (Sat_{soil})^\alpha\ \cdot LPS_{act} \,\,\,   [mm] </math>
-with:
+sendo que:
-Q<sub>LPS</sub>: Outflow from LPS [mm]
+Q<sub>LPS</sub>: fluxo de saída do LPS [mm]
-Sat<sub>soil</sub>: Relative water saturation of the soil at location [-]
+Sat<sub>soil</sub>: saturação de água relativa do solo no local [-]
-α : calibration coefficient [-]
+α : coeficiente de calibração [-]
-The advantage of this non-linear outfall function is that much less water runs off in low areal humidity than if it were a linear drain function. The common behavior of catchment areas which generate much more and faster runoff when there is high soil moisture (Baumgartner & Liebscher 1990; Dyck & Peschke 1995) than when there is low soil moisture (assuming the same precipitation amount) can be better displayed using an outfall function.
+A vantagem desta função de escoamento não linear é que muito menos água escorre em baixa humidade areal do que a de uma função de drenagem linear. O comportamento comum das zonas de captação que geram um escoamento muito maior e mais rápido quando há uma elevada humidade do solo (Baumgartner & Liebscher 1990; Dyck & Peschke 1995) do que quando há baixa humidade (presumindo a mesma quantidade de precipitação) pode ser exibido usando uma melhor função de escoamento.
-The gravitation water flowing out from the LPS (Q<sub>LPS</sub> ) is distributed among three different target storage. A certain amount goes to the middle pores and is stored there for a longer period of time, a second part percolates into the groundwater storage (vertical component) and the remaining amount provides the source for interflow (lateral component). The size of the components is subject to soil-physical parameters (especially kf values) and the slope of the corresponding HRU. Therefore, it is assumed in the model that the slope area generates much interflow, whereas in almost evenly situated locations the percolation into the groundwater is the main component. The amount which goes from large pores into middle pores is, however, subject to the saturation of the middle pore storage. In order to determine of runoff amounts the slope and two kf values have to be specified for each HRU: The kf value of the soil horizon with the lowest permeability and the kf value of the overlying horizon.
+A água de gravitação que flui para fora do LPS (Q<sub>LPS</sub> ) é distribuída entre três reservatórios de destino diferentes. Uma certa quantidade vai para o de poros médios e é armazenada aí durante um longo período de tempo, a segunda parte se infiltra no reservatório de água subterrânea (componente vertical) e a quantidade restante é a fonte para o interfluxo (componente lateral). O tamanho dos componentes está sujeito a parâmetros físicos do solo (especialmente valores kf) e a inclinação da HRU correspondente. Portanto, assume-se no modelo que a área de declive gera muito interfluxo, ao passo que em locais situados quase que interamente em planos, a percolação nas águas subterrâneas é o componente principal. A quantidade que vai de poros grandes a poros médios está, no entanto, sujeita à saturação do reservatório de poros médios. A fim de determinar os montantes de escoamento o declive e dois valores kf têm de ser especificados para cada HRU: O valor kf do horizonte do solo com a menor permeabilidade e o mesmo valor do horizonte sobrejacente.
-'''Percolation and interflow generation'''
+'''Percolação e geração de interfluxo'''
-A certain amount of available gravitation water seeps through the entire soil and contributes to groundwater recharge. In the model presentation of the J2000 this percolated amount is represented as dependent on the slope of the corresponding HRU. The slope influences the percolation in that inclined areas have a higher amount of gravitation water as lateral runoff from unsaturated zones, i.e. the groundwater recharge is less in these areas than in evenly situated locations. The influence of the slope is taken into account with a gradient according to the following equation:
+Uma certa quantidade de água de gravitação disponível se infiltra no solo inteiro e contribui para a recarga das águas subterrâneas. Na apresentação de modelo do J2000 esta quantidade percolada é representada como dependente da inclinação da HRU correspondente. A inclinação influencia a percolação na medida em que as áreas inclinadas têm uma maior quantidade de água de gravitação como escoamento lateral de zonas não saturadas, ou seja, a recarga é menor nessas áreas do que em locais situados em planos. A influência da inclinação é levada em consideração, com um gradiente de acordo com a seguinte equação:
 <math> grad_{perc} = (1 - tan \alpha)^\beta\  \,\,\, [-] </math>
-α: slope of the corresponding HRU [degree]
+α: inclinação da HRU correspondente [graus]
-β : shape parameter, calibration coefficient [-]
+β: parâmetro de forma, coeficiente de calibração [-]
-Using this equation the relation between vertical and lateral runoff is determined which can be adapted
+Ao usar-se esta equação da relação entre o escoamento vertical e lateral, determina-se o que pode ser adaptado para as condições na área de captação, com a ajuda do coeficiente de calibração β. Além disso, com este coeficiente de calibração pode ser melhorada a inclinação resultante de modelos de granulação grossa que é sistematicamente muito baixa.
-to the conditions in the catchment area with help of the calibration coefficient  β. In addition, with this
-calibration coefficient the slope resulting from coarse-grained models which is systematically too low can
-be enhanced.
-The water amount which is available for percolation is calculated according to:
+A quantidade de água disponível para a percolação é calculada de acordo com:
 <math> Perc_{pot}= grad_{perc} \cdot Q_{LPS} \,\,\, [mm] </math>
-This percolation rate is then set against the calibration coefficient ''soilMaxPerc'' which describes the
+Esta taxa de percolação é então definida levando em consideração o coeficiente de calibração ''soilMaxPerc'' que descreve a taxa de percolação máxima por intervalo de tempo.
-maximum percolation rate per time step.
-And for the interflow Interflow(RD2):
+E para o Interfluxo (RD2):
 <math> Interflow = 1- grad_{perc} \cdot Q_{LPS} \,\,\, [mm] </math>
-'''Runoff detention'''
+'''A retenção de escoamento'''
-Both runoff components, direct runoff (RD1) and interflow (RD2) are delayed in time in order to take into account the areal expansion of the spatial model entity. The detention takes place using corresponding retention coefficients (''soilConcRD1'', ''soilConcRD2''). The detention is calculated according to:
+Ambos os componentes de escoamento, de escoamento direto (RD1) e interfluxo (RD2) estão atrasados no tempo, com o objetivo de se considerar a expansão da área da unidade espacial do modelo. A retenção ocorre através de coeficientes de retenção correspondentes (''soilConcRD1'', ''soilConcRD2'').  Ela é calculado de acordo com:
 <math>RD1 = \frac{1}{soilConcRD1}  \cdot RD1{gen} \,\,\, [mm] </math>
@@ Linha 372: / Linha 368: @@
 <math>RD2 = \frac{1}{soilConcRD2}  \cdot RD2{gen} \,\,\, [mm] </math>
-Nepal (2012) suggested that in the case of RD1, the delayed time may be different during high-flow periods due to non-linear behavior of a catchment. Beven (2001a) highlighted that the non-linear responses primarily exist due to two causes. The first reason is the antecedent condition when the relationship between rainfall and runoff is generally considered to be nonlinear because the wetter the catchment prior to a unit input of rainfall, the greater the runoff that will be generated. Second, a non-linearity exists also due to change of velocity with discharge. Average flow velocities increase with the flow with both surface and subsurface flow processes. Faster flow velocities mean that the runoff will reach a measurement point in the stream-channel flow system more quickly. In case of high precipitation events (such as during the monsoon season in the study area) which are responsible for high flood peaks, a high degree of non-linearity is noted. During those events, the soil becomes saturated by the initial rainfall events and a higher rainfall-runoff coefficient is likely after some periods of rainfall. These typical conditions have been taken into account by introducing a new parameter into the J2000 modelling system. The new parameter (''concRD1Flood'') is used by the model when the RD1<sub>gen</sub> crosses a threshold value (''RD1FloodThreshold'') provided by a user. The value of (''concRD1Flood'') should be lower than concRD1 because it produces higher RD1 output flow.
+Nepal (2012) sugeriu que, no caso de RD1, o tempo de atraso pode ser diferente durante períodos de alto fluxo, devido ao comportamento não-linear de uma bacia. Beven (2001a) destacou que as respostas não-lineares existem principalmente devido a duas causas. A primeira é a condição antecedente, quando a relação entre a precipitação e o escoamento é geralmente considerada como sendo não-linear, porque quanto mais humidecida for a zona de captação antes de uma unidade de entrada (input) de precipitação, maior será o escoamento gerado. A segunda é a existência de uma não-linearidade também devido à mudança de velocidade com descarga. As velocidades de fluxo médias aumentam com o fluxo de superfície e com processos de fluxo abaixo dela. Velocidades de fluxo mais rápidas significam que o escoamento chegará a um ponto de medição no sistema de fluxo de canal mais rapidamente. No caso de ocorrência de precipitações extremadas (por exemplo, durante a estação de monções na área de estudo), que são responsáveis por picos de cheias elevadas, um alto grau de não-linearidade é observado. Durante esses eventos, o solo fica saturado com os acontecimentos iniciais de precipitação e um maior coeficiente de chuva-escoamento é provável após alguns períodos de chuva. Estas condições típicas foram levadas em conta, o que acabou na introdução de um novo parâmetro para o sistema de modelagem do J2000. O novo parâmetro (''concRD1Flood'') é usado pelo modelo quando o RD1<sub>gen</sub> cruza um valor limite (''RD1FloodThreshold'') fornecido pelo usuário. O valor de (''concRD1Flood'') deve ser mais baixo do que concRD1 porque produz um fluxo de saída RD1 mais elevado.
 <math>RD1_{flood} = \frac{1}{soilConcRD1Flood}  \cdot RD1{gen} \,\,\, [mm] </math>
-'''Diffusion'''
+'''Difusão'''
-At the end of the time step a deficit of the middle pore storage (MPS) resulting from evaporation be balanced out by water from the large pore storage (LPS). This diffusion ( diff) is carried out using the calibration coefficient ''soilDiffMPSLPS'' according to:
+No final do intervalo de tempo, um défice de um reservatório de poros médios (MPS), resultante da evaporação, é compensado pela água do reservatório de poros grandes (LPS). Esta difusão (diff) é levada a cabo utilizando o coeficiente de calibração ''soilDiffMPSLPS'' de acordo com:
-<math> diff = actLPS \cdot (1-e\frac{-1\cdot diff }{satMPS})  \,\,\, [mm] </math>
+<math> diff = actLPS \cdot (1-e\frac{-1\cdot diff }{satMPS})  \,\,\, [mm] </math>
-For more information see also: [Baumgartner & Liebscher 1990], [Dyck & Peschke 1995], [Gurtz et al.
+For more information see also: [Baumgartner & Liebscher 1990], [Dyck & Peschke 1995], [Gurtz et al. 1997], [Maniak 1997], [Menzel 1997], [Scheffer & Schachtschabel 1984], [Schulla 1997], [Uhlenbrook 1999], [Wessolek 1993].
-], [Maniak 1997], [Menzel 1997], [Scheffer & Schachtschabel 1984], [Schulla 1997], [Uhlenbrook
-], [Wessolek 1993]
 = Groundwater module =

Módulos do J2000 em detalhes

Revisão das 20h35min de 26 de Fevereiro de 2013

Índice

Módulo de distribuição de precipitação

Módulo de interceptação

Módulo de neve

Módulo de geleira

Módulo de água do solo

Groundwater module

Routing module

Vistas

Ferramentas pessoais

Navegação

Pesquisa

Ferramentas

Noutras línguas