Tutorium Monte Carlo Analyse
Der JAMS Data Explorer (JADE) bietet eine mächtige Werkzeugsammlung für die Monte - Carlo - Analyse von Umweltmodellen. Dies beinhaltet Methoden zur Sensitivitätsanalyse, Unsicherheitsanalyse und Visualiserung von Datensätzen, basierend auf der Monte - Carlo - Toolbox (MCAT), die von T. Wagener (??) entwickelt wurde.
Voraussetzung für die Anwendung der meisten MCAT Methoden ist ein vorangegangenes Monte - Carlo - Sampling, das heißt häufig wiederholte Anwendung des zu analysierenden Modells mit gestörten Parameter- und Eingabedaten. Um diese Aufgabe zu erfüllen existieren mehrere RandomSampler Komponenten, die ausführlicher hier [?] erklärt werden.
Das Resultat des Samplings ist eine Zusammenstellung der Modellantworten, die aus Modelparametern, Gütekriterien, skalaren Modellergebnissen sowie räumlichen und zeitlich aufgelösten Datensätzen bestehen können.
Bei der Arbeit mit Ensembles entstehen oft riesige Datenmengen, deren Verarbeitung hohe Rechenzeit- und Speicheranforderungen bedarf. Da, das allgemeine JAMS Datenkonzept hierbei an seine Grenzen stößt, wurde mit Hinblick auf
- Effiziente Datenspeicherung unter Berücksichtigung des Speicherbedarfs
- Schnelle und einfache Erstellung von Ensembles aus Rohdaten
- Flexibilität und Erweiterbarkeit im Sinne von Datentypen
- Einbettung von Metadaten
entwickelt.
Um einen Ensemble Datensatz zu erstellen, wird wie folgt vorgegangen.
Wählen Sie im Menü Datei den Eintrag Erzeuge Ensemble. Sie sehen nun folgenden Dialog
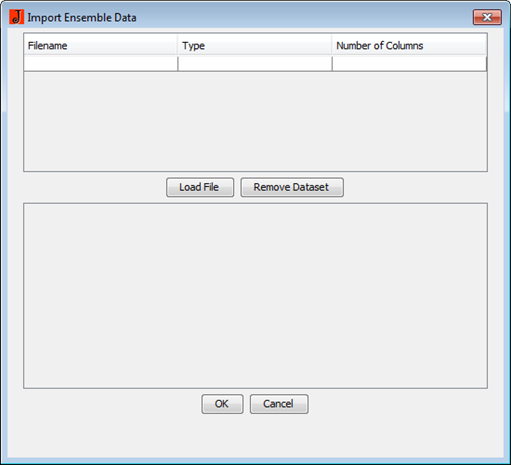
Klicken sie nun auf die Schaltfläche Laden um eine JAMS-Modellausgabendatei (z.b optimizer_wizard_J2K.dat) auszuwählen. Nachdem Sie eine Datei gewählt haben, werden alle enthaltenen Datensätze aufgelistet. MCAT unterscheidet zwischen vier verschiedenen Datentypen: Parameterwerten, Gütekriterien, skalaren Modellausgaben und simulieren und beobachteten Zeitserien. Da diese Information nicht explizit in den Modellausgaben enthalten ist, müssen Sie diese angeben.
Allerdings sind für viele Anwendungen bereits Standardwerte hinterlegt, die die Arbeit erleichtern.
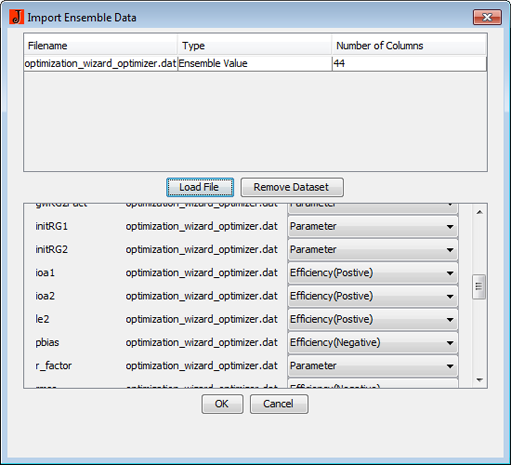
Sie können beliebige weitere Datensätze zu dem Ensemble hinzufügen. Achten Sie aber darauf, dass nicht jede Zusammenstellung semantisch korrekt ist. Zum Beispiel ist die Verknüpfung von unterschiedlichen Monte - Carlo - Samplings ist im Allgemeinen nicht sinnvoll. Zum Abschluß beenden Sie den Dialog mit "OK". Sie werden nun aufgefordert die Ensemble-Datei zu speichern. Speichern Sie diese im gleichen Verzeichnis in dem sich auf die anderen Modellausgaben befinden (z.B. workspace\output\current\) Öffnen Sie nun den entsprechenden Workspace und klicken sie doppelt auf die Ensembledatei. Es öffnet sich nachfolgende Unterfenster, welches die wichtigsten Informationen über das Ensemble liefert. Dazu gehören die vorhandenen Datensätze, die Anzahl der Monte - Carlo - Simulationen, der abgedeckte Modellierungszeitraum und der verwendete Monte - Carlo - Sampler.
Im Nachfolgenden werden die verfügbaren Werkzeuge in Kurzform vorgestellt.
Dotty Plot
Anwendung: Modellidentifikation, Sensitivitätsanalyse
Inputdaten: Parameter, Gütekriterium
Ein Modellparameter ist als identifizierbar definiert, wenn alle geeigneten Parametrisierungen in einem relativ kleinen Bereich des gültigen Parameterintervalls liegen. Unter geeignete Parametrisierung ist hierbei eine Parameterkombination zu verstehen, die zu plausiblen Modellantworten führt. Ein Modell ist identifizierbar, sofern dessen Parameter alle identifizierbar sind. Diese erlaubt die eindeutige Bestimmung dieser mit Hilfe der Eingabe- und Messdaten.
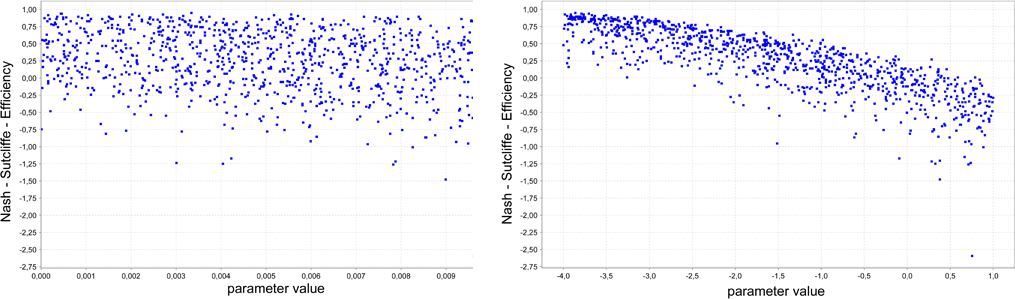
Ein Dotty Plot ist ein spezielles Streudiagramm zur Prüfung auf Parameter - Identifizierbarkeit und Sensitivität. Jeder Punkt repräsentiert ein Gütekriterium, das mit einer speziellen Parameterkombination erzielt wurde. Für die Visualisierung wird der Parameterraum durch Auswahl eines Parameters auf eine Dimension projiziert. Die restlichen Parameter werden dabei ignoriert. Die obere Kante der Punkte repräsentiert eine Nährung für die beste Modellrealisation, die mit einem bestimmten Wert des ausgewählten Parameters erzielt werden kann. Falls diese Linie ein wohldefiniertes Maximum in einem schmalen Intervall aufweist, kann der Parameter als gut identifizierbar eingeordnet werden. Die beiden Abbildungen zeigen einen gut identifizierbaren eunen nicht identifizierbaren Parameter.
Dabei muss angemerkt werden, dass viele Modelle nicht oder nur teilweise identifizierbar sind. Oft können sehr unterschiedliche Parametrisierungen eine geeignete Erklärung für ein System bieten. Dies ist unter dem Begriff Equifinalität bekannt. Der wesentliche Grund für das Auftreten von Equifinalität ist, dass unterschiedliche interne Modellzustände ähnlichen Modellantworten hervorrufen können. Wäre es möglich alle Modellzustände zu validieren, würde das Problem nicht auftreten, da dies aber in der Praxis unrealistisch ist, ist es unmöglich zu entscheiden, welche Modellparametrisierungen tatsächlich korrekt sind und welche zurückgewiesen werden können. Als logische Konsequenz sollte jede Parametrisierung in der Simulation berücksichtigt werden, die nicht ausgeschlossen werden kann.
A Posteriori Parameter Distribution
Anwendung: Modellidentifikation
Inputdaten: Parameter, Gütekriterium
Der A Posteriori Parameter Distribution Plot kann mit Hilfe des Dotty Plots beschrieben werden. Zunächst werden die Gütewerte der Parameter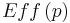 
normiert, so dass sie als Wahrscheinlichkeit 
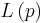interpretiert werden können. Damit gilt für L(p)
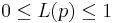
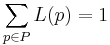
- Fehler beim Parsen (Unbekannter Fehler): L(p)<L(p') \ Eff(P) schlechter \ als \ Eff(p') \
Die Parameterachse des Dotty Plots wird in mehrere gleich große Teilintervalle zerlegt. Jeder Punkt des Dotty Plots wird nun seinem entsprechendem Intervall zugeordnet. Für jedes Intervall Ik wird die durchschnittliche Wahrscheinlichkeit der zugehörigen Punkte berechnet.
Das entstehende Balkendiagramm stellt damit die Wahrscheinlichkeit dar, dass der wahre Wert von p in dem entsprechenden Intervall liegt. Ein Maximum Likelihood Schätzer würde nun, das Interval mit maximalen Wert als beste Schätzung für den Parameter annehmen.
Ist der Parameter identifizierbar, sollte ein Balken mit hoher Wahrscheinlichkeit herausstechen. Die beiden Abbildungen zeigen einen identifizierbaren und einen nicht identifizierbaren Parameter.
Datei:A posteriori plot
