Set Evaluation criteria

From ILMS-Wiki
Jump to: navigation, search

It is necessary to have evaluation criteria, to judge the efficiency of an simulation. Evaluation Criteria quantify the similarity of two timelines. Evaluationcriteria are used to check the quality of an simulation. Although they quantify the simularity of two timelines. That makes it an objective measure instrument for variance of a timeline when observated and on the other hand enable to make an evaluated comparisson of errorfunctions between multiple timelines with the focus on observation. It is an goal of automated calibriation to change modellparameters in that way, that the simularity of an simulated timeline to an observated timeline, get maximized. For this process are errorfunctions essential. There exists countless measures, to evaluate the modell performance, that execl through there individual pro and contras. Usually used measures are:


Contents

prozentualer Volumenfehler (PBIAS)

Measures the relative error between the simulated and the observated timeline. This measure shows, if the simulation follows a systematically over or unter rating.

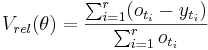
{V_{rel}(\theta)} = { {\sum_{i=1}^r (o_{t_i} - y_{t_i})} \over {\sum_{i=1}^r o_{t_i}}}

Nash-Sutcliffe-Effizienz(E2)

The Nash-Sutcliffe Effizienz E2 (Nash und Sutcliffe, 1970)

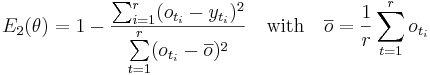
E_2 (\theta) = 1 - { \sum_{i=1}^r (o_{t_i} -y_{t_i})^2 \over \sum\limits^{r}_{t=1} ( o_{t_i}- \overline o )^2 } \quad \mathrm { with} \quad \overline o = \frac {1}{r} \sum\limits^{r}_{t=1} o_{t_i}


is definated as one monus the sum of absolute quadratic aberration, that will be normalized with the variance of observation in the viewed period. The range of the Nash-Sutcliffe efficience reaches from minus till plus one. It has its maxiums if both timelines are in conform. An negativ value means, that the modell rated the observation less than the middlevalue of observation. E2 is used very often, but has some disadvantages. Aberrances are quadratic calculated, therefore are higher drainvalues stronger judged than lower drainvalues. But as an result it is perfectly used for evaluation of highwaterperiods and drainpikes (Legates and McCabe Jr, 1999). Schaefli and Gupta (2007) made a point, that E2 depends from the statistical spread of the timelines and therefore is only areaspecificaly. Thats why the Nash-Sutcliffe efficience can only be used restricted to compare different areas.

The modified Nash-Sutcliffe Effizienz E1

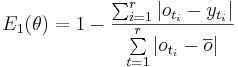
E_1 (\theta) = 1 - { \sum_{i=1}^r \left |o_{t_i} -y_{t_i} \right | \over \sum\limits^{r}_{t=1} \left | o_{t_i}-\overline o \right | }


has simulare properties as the usual Nash-Sutcliffe efficience. The difference is that the aberrance is quantified with the usual absolute value function. So can be an overproportional weighting of drainpikes be denied. This error function provides an balanced evaluation for the simulation (Krause et al., 2005).

logarithmic Nash-Sutcliffe-Effizienz (logE2)

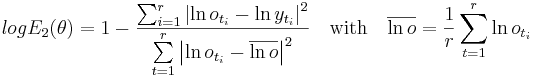
logE_2 (\theta) = 1 - { \sum_{i=1}^r \left |\ln o_{t_i} -\ln y_{t_i} \right |^2 \over \sum\limits^{r}_{t=1} \left |\ln o_{t_i}-\overline {\ln o} \right |^2 } \quad \mathrm { with} \quad \overline {\ln o} = \frac {1} {r} \sum\limits^{r}_{t=1} \ln o_{t_i}

is used to make an logarithmic transformation of the values. So that higher values (e.g. drainpikes) are more flatened and lower values have more weight in the simulation. (Krause and Flügel, 2005).

Determinationvalue

The determinationvalue R2 measures the intensity of linear connections between observated and simulated timelines. The valuerange of this value is between 0 and 1. There is an perfect linear connection between observated and simulated timelines, if the value is 1 or 0. There is no linear connection if the value of R2 is 0. The determination value doesn't valuate two timelines for there quantity conformity. It only checks there dynamics are alike. It is not recommendet to valuate hydrographs alone with this measure (Krause et al., 2005). The determinationvalue is define as the square of the empiric correalationcoefficient of both timelines:


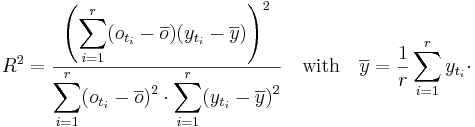
R^2 = {\left ( \displaystyle \sum_{i=1}^r (o_{t_i} -\overline {o} ) (y_{t_i} -\overline {y} ) \right)^2 \over \displaystyle \sum_{i=1}^r (o_{t_i} - \overline {o})^2 \cdot \displaystyle \sum_{i=1}^r (y_{t_i} - \overline {y})^2 } \quad \mathrm {with} \quad \overline {y} = \frac {1} {r} \displaystyle \sum_{i=1}^r y_{t_i} \cdot

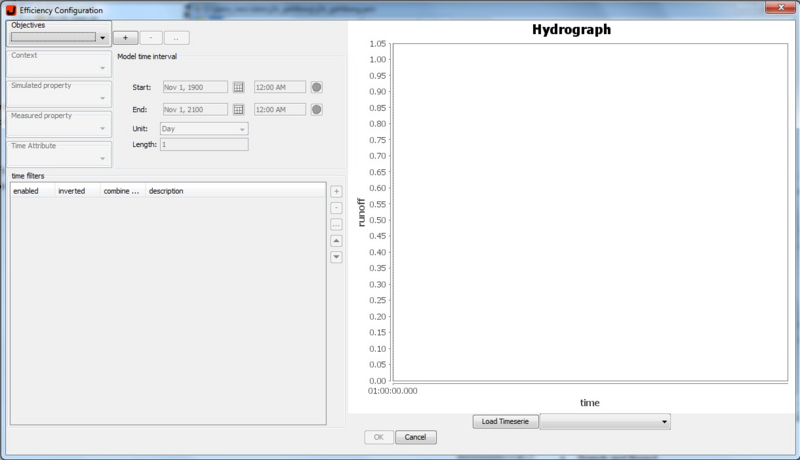
Set evaluation criteria with the aid of JAMS Model Builder

You can find this option in the tab Configure Efficiencies. Now you should see the following window:

hier ist ein Bild
Gütemaße konfigurieren


Now you can set , depending on your requirements of your callibration, criteria. As an example we show you here an minimal configuration :
1. step: Click on the button "+" , to create a new criteria.
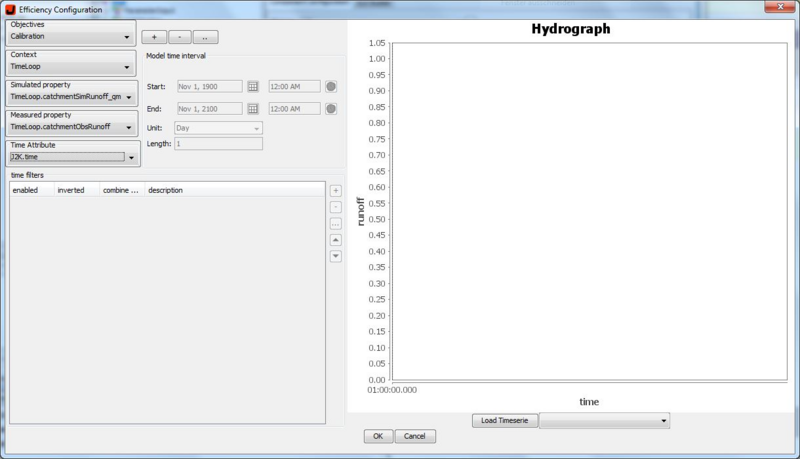
2. step: Specifiy your attributs, that you want to compare. Both attributs must be set in the same contextcomponent. First chose from the drop-down-list the needed context, second the measured/observed and simulated attribut.

3. step: Chose an attribut, which represents the aktuell timestep of the simulation. Often, it should be "TimeLoop.time". You should see a similar window like this:

hier ist ein Bild
Gütemaße konfigurieren

4. step: click on OK to integrate the evaluation criteria to your model.

Retrieved from "https://jams.uni-jena.de/ilmswiki/index.php/Set_Evaluation_criteria"
Personal tools