From ILMS-Wiki

Jump to: navigation, search

This tutorial describes the important processes and algorithm of the different modules within the J2000 hydrological model in detail:

Precipitation distribution module

Calibration parameters

parameter	description	Global range	For Dudh Kosi model
Trans	threshold temperature	0 + 5	2
Trs	base temperature for snow and rain	-5 +5	0

In the J2000 modelling system, the precipitation is first distributed between rain and snow depending upon the air temperature. Two calibration parameters (Trans, and Trs) are used where Trs is base temperature and Trans is a temperature range (upper and lower boundary) above and below the base temperature. In order to determine the amount snow and rain, it is assumed that precipitation below a certain threshold temperatures results in total snow precipitation and exceeding a second threshold results in total rainfall as precipitation. In the range (Trans) between those threshold temperatures, mixed precipitation occurs. Between those thresholds, rain-snow mixtures with variable percentages for each component are calculated. The acutal amount of snow (P(s)) of daily precipitation subject to air temperature is calculated according to:

Failed to parse (unknown error): Ps = \frac{Trs + Trans - T}{2 \cdot Trans} \mathrm{[mm]}

The daily amount of snow (P_s) or amount of rain (P_r) is calcualted according to:

$Ps = Precipitation \cdot Ps \,\,\, \mathrm{[mm]}$

$Pr = Precipitation \cdot (1- Ps) \,\,\, \mathrm{[mm]}$

These parameters are considered as non-flexible parameters and not necessarily placed in the JAMS framework as tunable parameters.

Relevancies in modelling

Putting the Trs values below zero (e.g. 2) will bring more precipitation in the form of 'rain' than 'snow'.

Interception module

Interception is a process during which the precipitation is stored in leaves, and other open surfaces of vegetation. During precipitation, interception by crop canopy and residue layer occurs. This process is identified as important components of a hydrological cycle that can affect the water balance components. Canopy and residue interception are considered losses to the system, as any rainfall intercepted by either of these components will subsequently be evaporated (Kozak et al. 2007). The interception module in the J2000 modelling system serves the calculation of the net precipitation from the observed precipitation against the particular vegetation covers and its development in the annual cycle. The observed precipitation is reduced by the interception part to calculate the net precipitation. Thus net precipitation only occurs when the maximum interception storage capacity of the vegetation is reached. The surplus is then passed on as throughfall precipitation to the next module. The interception module uses a simple storage approach according to Dickinson (1984), which calculates a maximum interception storage capacity based on the Leaf Area Index (LAI) of the particular type of land cover. The emptying of the interception storage is done exclusively by evapotranspiration. The maximum interception capacity (Int_max) is calculated according to the following formula:

$Int_{max} = \alpha \cdot{LAI} \, \, \, \mathrm{[mm]}$

with

α ... storage capacity per m² leaf area against the precipitation type [mm]

LAI ... LAI of the particular land-use class provided in land-use parameter file [-]

The parameter a has a different value, depending on the type of the intercepted precipitation (rain or snow), because the maximum interception capacity of snow is noticeably higher than of liquid precipitation. The LAI for individual vegetation types is provided in the land-use parameter file throughout the year. Because the LAI changes according to the seasons, four different LAI types for four different seasons for each vegetation type are proposed in land-use parameter file. The value of LAI can be determined by direct measurement of leaves, literature, and expert knowledge.

Snow module

Calibration parameters

parameter	description	Global range	For Dudh Kosi model
snowCritDens	Critical density of snow	0 to 1	0.381
snowColdContent	cold content of snowpack	0 to 1	0.0012
baseTemp	threshold temperature for snowmelt	-5 to 5	0
t_factor	melt factor by sensible heat	0 to 5	2.84
r_factor	melt factor by liquid precipitation	0 to 5	0.21
g_factor	melt factor by soil heat flow	0 to 5	3.73

These parameter are provided in bold and italic letters in the description below:

The snow module calculates the different phases of snow accumulation, metamorphosis and snowmelt. The more complex module is adapted in the model from Knauf (1980). The snow module takes into account the changes of state of snow pack during its existence, especially changes of snow density due to melting and subsidence. This process is important because snow pack can store free water, like a sponge, until reaching a certain threshold density and only then a sudden discharge of water occurs. For the model different water capacities of the snow pack are considered: the actual snow water equivalent (SWE_dry) which corresponds to the amount of water which has actually frozen and the total snow water equivalent (SWE_total) which in addition considers liquid water stored in the snow pack. The subsidence of the snow pack, which results from the liquid water through the snowmelt to the surface or from precipitation as rainfall, is calculated according to the empirical subsidence (snow-compaction scheme) by Bertle (1966).

The snow pack and its conditions are described in the modell according to the following parameters: snow depth (SD)[mm], dry snow density (dryDens)} [in g/cm³] as the quotient from total water content and snow depth.

If there is minimum, mean or maximum air temperature for a certain time (daily data), the module calculates separate accumulation or melt temperatures. Accumulation and melting can occur within a time step. The accumulation and melt temperatures (T_acc and T_melt) can be calculated according to:

$T_{acc} = \frac{T_{min} + T_{avg}}{2} \,\,\,\,\,\,[^oC]$

$T_{melt} = \frac{T_{max} + T_{avg}}{2} \,\,\,\,\,\,[^oC]$

Accumulation phase:

The snow module simulates accumulation and compaction of the snow pack caused by snowmelt or rain on snow precipitation.

The thermal circumstances under the snow cover are taken into account with the cold content in the snow cover in connection with the snowmelt. At the temperature below the freezing point, the snow pack cools down significantly. Because melted water freezes immediately due to negative isothermal circumstances under the snow cover, no runoff occurs. The cold content needs to reach the value zero so that the process of snowmelt begins again. Consequently, negative temperatures raise the cold content whereas the positive temperature reduces it. The calculation of storage of cold content results from the product of air temperature by a calibration parameter (coldContFact).

$CC = coldContFact \cdot T \,\,\,\,\,\,[mm]$

In doing so, negative air temperatures are accumulated and decreased only by positive temperature and resulting potential rates of melting. Only when the cold content has reached a value of 0, snowmelt occurs.

If the air temperature is below -15 C, the density of the new snow is assumed to be 0.02875.

The change of snow depth (δ SD) resulting from snow precipitation is calculated according to : Snow accumulation occurs in the model if precipitation falls in solid form (newSnow > 0). Therefore the density of new snow is determined subject to air temperature. The calculation is carried out according to (Kuchment 1983, and Vehvilaeinen 1992), if the air temperature is higher than -15 oC.

$newSnowDens = 0.13 + 0.0135 \cdot T_{acc} + 0.000045 \cdot T^{2}_{acc}\,\,\,\, [g/cm^3]$

If the air temperature is below -15 oC, the density of the new snow is assumed to be 0.02875.

The change of snow depth (δ SD) resulting from snow precipitation is calculated according to :

$δ SD = \frac{netSnow}{newSnowDens} \,\,\,\,\,\,[mm]$

The snow water equivalent of the previous day (\textit{SWEdry}) increases by the value of snow precipitation according to:

$SWEdry_{{t}} = SWEdry_{{t-1}} + netSnow \,\,\,\,\,\,[mm]$

The dry snow water equivalent and the total snow water equivalent are increased by the same value. If the precipitation event involved mixed (rain/snow) precipitation, the rain amount is allocated to the total snow water equivalent.

If rain is part of the precipitation event, it results in subsidence of the snow pack. The calculation of the subsidence amount is discussed below. In the model, the snow pack remains in the accumulation phase until the temperature value (T_melt) for the snowmelt exceeds a threshold value (baseTemp)which has to be determined during the parameterisation phase of the modeling application. Then it enters the metamorphosis phase which simulates melting and subsidence processes. However, it can go back to the accumulation phase if temperatures are correspondingly low. Due to different temperature values, accumulation and melting processes can be modeled during one time step.

Melting and subsidence phase:

If the melt temperature value (T_melt) exceeds the temperature limit value (baseTemp), the snow pack goes from the accumulation phase to the metamorphosis. The amount of energy which is required for snowmelt is available in three different ways. First, by input of sensible heat by air temperature (t_factor), second, by energy input from precipitation as rain (r_factor) and third, by input due to soil heat flow (g_factor). The sum of all energy inputs gives the potential snowmelt rate (Mp). The calculation of Mp is carried out according to:

$Mp = t\_factor \cdot T_{melt} + r\_{factor} \cdot netRain \cdot T_{melt} + g\_{factor} \,\,\,\,\,\,[mm]$

The variable Mp is then also modified according to the slope and the exposition of the spatial model entity (i.e. HRU):

$Mp = \ Mp \cdot actSlAsCf \,\,\,\,\,\,[mm]$

Mp is initially used to balance out the cold content of the snow cover and is then also used to generate snowmelt. The potential snowmelt rate then is taken to calculate the resulting maximum change of snow depth (δ SD):

$δ SD = \frac{M_P}{dryDens} \,\,\,\,\,\,[mm]$

If δ SD is greater than the entire snow depth, it defrosts completely and the entire snow water equivalent contributes to runoff generation in the form of snowmelt. If this is not the case, the snow depth is reduced correspondingly, which does not change the snow water equivalent at first. Rather the result is an increase in the total density of the snow cover.

In addition to this change in density, additional changes in subsidence and density according to the snow compaction-scheme (Bertle 1966) are taken into account. This method is based on the fact that water, no matter whether it results from temperature-induced snowmelt or from precipitation, seeps into the snow pack which leads to subsidence by recrystallization of snow and by structural changes and concentration in the storage (Knauf 1980). The resulting subsidence rate is calculated using the snow-subsidence method described in Bertle (1966). This method is based on the observation of an empirical relation between inflowing free water and the resulting change in elevation by subsidence which was derived from laboratory experiments of the US Bureau of Reclamation. For the calculation the increase of accumulated water content in percentage is seen in relation to the snow water equivalent using this formula:

$P_w = \frac{totSWE}{drySWE} \cdot 100 \,\,\,[\%]$

This equation shows that the more liquid water there is as input, the greater is the snow pack subsidence (P\_w) (Knauf 1980). An input of the exact the amount of water corresponding to the snow water equivalent of the snow pack leads to halving the snow depth by subsidence. The percentage of snow depth change (P$_H$) is calculated subject to the input of free water:

$P_H = 147.4 - 0.474 \cdot P_W \,\,\,[\%]$

The new snow depth (SD) is:

$SD = SD \cdot \frac{P_H}{100} \,\,\,[mm]$

Together with the snow depth which has been calculated the total density \textit{(totDens)} and the dry snow density \textit{(dryDens)} are calculated according to the following formulas:

$dryDens = \frac{SWE_{dry}}{SH} \,\,\,[g/cm^3]$

$totDens = \frac{SWE_{tot}}{SH} \,\,\,[g/cm^3]$

Melt runoff

The snow pack can store liquid water in its pores up to a certain critical density (snowCritDens). This storage capacity is lost nearly completely and irreversibly when a certain amount of liquid water in relation to the total SWE (between 40 and 45 percent) is reached according to Bertle (1966), Herrmann (1976) and Lang (2005). In this threshold limit, the retention capacity of a naturally developing snow pack is also suddenly decreased without rain impact. In such a case, a sudden water release from the snow pack can be observed (Herrmann 1976). In the model, this process is simulated by using the calculation of a maximum water content of the snow pack (SWE_max) according to :

$WS_{max} = snowCritDens \cdot SD \,\,\,\,\,\,[mm]$

The critical density (snowCritDens) needs to be provided by the model user. The water stored in the snow pack which exceeds this limit is conveyed as snow runoff (Q_snow).

$Q_{snow} = SWE_{tot} - SWE_{max} \,\,\,\,\,\,[mm]$

In the following time steps, the density of the snow pack keeps the critical threshold density until it is either defrosted or starts the accumulation due to recurring snowfall.

Glacier module

The glacier module is developed and adapted as a part of the PhD research (Nepal, 2012) carried out in the Dudh Kosi river basin. The information provided here is taken from this study.

The glacier module is integrated into the standard J2000 hydrological model, as a part of this study. The glacier module is treated as a separate module within J2000 in which snow- and ice- melt (SIM) runoff is estimated and the output is directly provided to a stream as overland flow (RD1). The approach suggested by Hock (1999) is implemented in the J2000 model and further adapted for icemelt estimation. This approach considers ice melt by using a day-degree-factor. From this study, slope, aspect and debris-covered factors are further included in the model for ice-melt runoff. The melting of snow in the glacier area is calculated in the same way as described earlier. The same soil heat flux (calibration parameter: g_factor) is proposed for the snowmelt in glacier areas as most of the glaciers are debris-covered and behave similar to soil.

The glacier area is provided as a GIS layer which provides a unique land-use ID for glaciers during HRU delineation. All the processes which occur in the glacier are separately treated based on the unique ID. First the seasonal snow occurs on top of the glacier (or glacier HRU). The model first treats the snow as described in the 'Snow Module" and produces snowmelt runoff. In order to make sure that ice melt occurs, two conditions have to be met. First, the entire snow cover of a glacier HRU has to be melted (i.e.storage is zero), and second, the base temperature (tbase) as defined by users, has to be less than meltTemp. Only under these circumstances, the ice melt occurs as a model progress.

$meltTemp = \frac {Tmax + Tmean} {2} \,\,\,\,\,\,[^oC]$

The melt rate for glacier ice (iceMelt) (mm/day) is obtained by the following equation:

$iceMelt = \frac{1}{n} \cdot meltFactorIce + alphaIce \cdot radiation \cdot (meltTemp - tbase) \,\,\,\,\,\,[mm]$

where:

radiation = actual global radiation

meltFactIce = generalized melt factor for ice as a calibration parameter

alphaIce = melt coefficient for ice

n = time step (i.e. for daily model, n=1)

The ice melt is further adapted by the debris covered factor. Because the glaciers in the Dudh Kosi river basin are in general debris cover, a simple segregation method is applied to identify debris-covered glaciers based on slope. If the slope is higher than 30 degrees, the gravels, stones and pebbles are rolled down and the glacier is regarded as a clean glacier. The slope lower than this threshold is suitable for the accumulation of debris on top of glaciers. By using this approach, about 77 percent of the glaciers are estimated as debris-covered glaciers. According to Mool (2001a), about 70 percent of the glaciers in the Dudh Kosi river basin are valley types. One of the most common characteristics of glaciers located in the Himalayan region is the presence of debris material. In general, valley glaciers are debris-covered in the Himalayan region (Fujji 1977; Sakai2000}. It can be assumed that the debris-covered glacier areas estimated by this approach are fairly representative and adequate for purposes of this modelling application.

The presence of debris affects the ablation process. Supra-glacial debris cover, with thickness exceeding a few centimeters, leads to considerable reduction in melt rates (Oestrem 1959; and Mattson 1993). According to (Oestrem 1959) the melt rate decreased when the thickness of the debris cover was more than about 0.5 cm thick. The report further mentioned that not only the melting will be slower under the moraine cover, but also the ablation period will be shorter for the covered ice. The clean glaciers as reported on the Tibetan Plateau have higher retreat rates. (Kayastha 2000) studied the ice-melt pattern in the Khumbu glaciers (Dudh Kosi river basin where the J2000 model is being applied) and found that the debris ranging thickness from 0 to 5 cm indicates that ice ablation is enhanced by a maximum at 0.3 cm. Therefore, when a glacier is covered by debris, the ice melt is reduced. Using the calibration parameter (debrisFactor), the effects of debris cover on melt is controlled as follows.

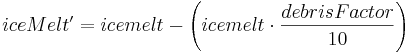
$iceMelt' = icemelt - \left(icemelt \cdot \frac{debrisFactor}{10}\right)$

The icemelt is further adapted with the slope and aspect of the particular glacier HRU. Routing of glacier melt is made separately for snowmelt, ice melt and rain runoff using the following formula:

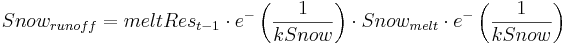
$Snow_{runoff} = meltRes_{t-1} \cdot e^ -\left(\frac {1}{kSnow}\right) \cdot Snow_{melt} \cdot e^ -\left(\frac {1}{kSnow}\right)$

where:

snow_melt = total snowmelt during the time step (mm/day)

meltRes_t-1 = outflow of reservoir during the last time step

kSnow = storage coefficient (recession constant) for reservoir

A similar routing procedure is applied for ice melt and rain runoff with a different recession constant (kIce) and (kRain). It is assumed that the routing of rain runoff is faster than that of ice and snow.

In reality, snow is stored in the accumulation zone of high-altitude areas. The snow is transported to low-altitude by wind, avalanches and gravity. As snow gets buried under new snow, it is gradually converted into firn and eventually into glacier ice. This ice flows by gravity downstream towards the ablation zone as glaciers (Jansson 2003). However, such dynamic processes of snow transformation and transportation are not included in the glacier module of the J2000 model. Therefore, some part of the precipitation is always stored as snow in the accumulation zone of high-altitude areas. To compensate for this long-term storage process, a constant glacier layer is used as a surrogate which provides melting from glacier ice.

Soil water module

The description of the soil water module as described in model source code is provided here which is primarily based on the technical documentation of the J2000 model (Krause, 2011).

In the soil module separate soils are represented according to their pore volumes. The pore storage which can occur in the soil are classified in the literature as follows (e.g. (Scheffer & Schachtschabel 1984)):

The water stored in fine pores (< 0.2 μm diameter, pF > 4.2, corresponds to the permanent wilting point - PWP) is so strongly bound due to its adsorption powers that it is not at all available for runoff generation.

The water stored in middle pores (diameter 0.2 to 50 μm, pF 1.8 to 4.2, corresponds to usable field capacity -nFk) is hold against gravity due to its adsorption powers. It can be extracted from the soil almost exclusively by using suction potential.

The water stored in coarse and macro pores (> 50 μm diameter, pF > 1.8, corresponds to air capacity - Lk) is subject to gravitation and can be kept in the soil for only a short period of time (1 to 2 days according to (Scheffer & Schachtschabel 1984).

The water stored in the fine pores can be neglected during the modeling as it is not available for evaporation or flow processes according to the above-mentioned specification of the pore volumes due to the constant binding. Hence the modeling abstraction of the soil is carried out by two parallel and connected storage in the model J2000: one storage which corresponds to the middle pore storage volume (hereinafter referred to as MPS) and which can only be emptied by evaporation and another storage which represents the volume of the large and macro pore storage (hereinafter referred to as LPS) and which is the source for the actual runoff.

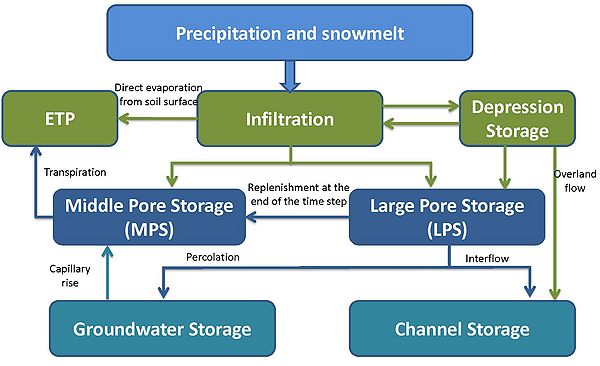
The figrue below shows the imporatant hydrological processes within the soil zone. It can be seen that an infiltration storage precedes the soil storage which contains net precipitation and water resulting from snow melt. From this storage the water is distributed to both soil storage where remaining water is cached in the depression storage in case of exceeding a maximum infiltration capacity of the corresponding soil or a saturation of the large pore storage. Emptying the depression storage is done by evaporation, the generation of surface runoff and/or seepage at a later point in time. Emptying the middle pore storage is done by evapotranspiration, emptying the large pore storage by generating interflow or by groundwater recharge. In addition, at the end of the time step a certain amount of the water stored in large pores can be transferred to the middle pore storage. The middle pore storage can, in addition to this water amount and to the infiltration, receive water from the saturated zone due to capillary rise. These individual processes are explained in detail below, however the parameterization of the soil module is discussed beforehand.

Infiltration

The first process which contains the water resulting from the snow melt and from net precipitation is infiltration. Whether water can seep away entirely or whether it is stored for a short time at the surface and whether it generates depression storage at this place or surface runoff, is subject to the infiltration capacity of the corresponding soil. The infiltration capacity is calculated by a simplified method which is suitable for daily time steps. It is based on the assumption that infiltration capacity is on the one hand subject to water saturation in the soil and on the other hand it cannot exceed a certain threshold value, a maximum infiltration rate. If this maximum infiltration rate is set to a constant mean value for the whole year, there are two problems, at least for two special cases:

In convective precipitation with high intensities and short duration. Often the infiltration capacity of the soil is exceeded since much water comes to the soil within a short time although the precipitation amount for the whole day would not imply this.

In snow melt runoff from the snow cover. Although water is released in a quite continuous manner, the soil behaves like a sealed area since it is partly or completely frozen or since water runs off within the snow cover without having the chance to seep away.

In order to take these special cases into account, at least rudimentarily. Two threshold values can be indicated in addition to the "standard value". Since special case 1 occurs mainly in summer months, a threshold value can be specified for summer half year. This threshold value serves to take into account thundershowers with high intensity within a short time which occur mainly during summer months. The second threshold value is applied if the modeled unit is covered in snow. Using this value the reduced infiltration capacity of the soil with a partly or completely frozen surface is considered. At the same time this value can be used to take into consideration the runoff of melt and precipitation water within the snow cover. The third value represents the standard case and therefore holds for the winter half year and for entities without snow cover.

The threshold values which are to be determined by the user (soilMaxInfSummer, soilMaxInfSnow, soilMaxInfWinter referred below in the equation as soilMaxInf1,2,3) are weighted during the modeling with the relative saturation deficit of the soil (δ_sat). The resulting maximum infiltration rate ( Inf_max) then calculated according to:

$Inf_{max} = soilMaxInf_{1, 2, 3} \cdot (1 - satSoil) \,\,\, [mm/d]$

The relative water saturation of the soil can be calculated using:

$soilSat = \frac{actMPS + actLPS}{maxMPS + maxLPS} \,\,\, [mm/d]$

If the water amount of precipitation and snow melt for the infiltration exceeds the calculated maximum infiltration rate, the excess is transferred to the depression storage and cached there. The resulting, actually seeping water amount (Inf_act ) is distributed among the soil storages. The amount of water which is in every soil storage is subject to the saturation deficit of the middle pore storage (MPS) and is calculated using the calibration parameter soilDistMPSLPS as follows:

The large pore storage (LPS) receives remaining water according to:

$MPS_{in} = Inf_{act} \cdot \frac{1 \cdot soilDistMPSLPS}{satMPS} \,\,\, [mm]$

The large pore storage (LPS) receives remaining water according to:

$LPS_{in} = Inf_{act}-MPS_{in} \,\,\, [mm]$

Due to the water distribution according to these equations the middle pore storage works like a sponge and its potential of taking water increases with increasing dehydration. However, a certain amount always remains in the large pore storage. The weighted distribution has the advantage that even in dry soils, especially during the summer months, part of the infiltrated water can run off fast. If the water was not distributed, interflow could only occur after saturating the middle pore storage, i.e. after achieving usable field capacity. Various investigations showed that large and macro pores can also achieve runoff if there is no water saturation in the soil.

Other special cases of infiltration occur with sealed areas and water areas. For water areas the water which is actually available for infiltration is transferred to an individual storage which can only be emptied by evaporation. In sealed areas only a certain amount of water on the surface seeps away subject to the degree of sealing (e.g. 25% with degree of sealing > 80% and 60% with degree of sealing < 80% according to (Wessolek 1993). The remaining part contributes to the total runoff in the form of surface runoff. This is considered by using corresponding coefficients (soilImpGT80, soilImpLT80) which have to adjusted by the user.

The depression storage

As represented in the description of infiltration above, the water amount which exceeds the maximum infiltration rate of the soil is transferred to the depression storage. This also applies if the soil is completely water-saturated and no infiltration can take place. The water which is stored in the depression storage runs off partly as surface runoff. The maximum amount in mm m{-2} which can be kept as depression storage on the individual are has to be indicated during model parameterization. According to Maniak (1997) the maximum depression storage lies between 0.6 and 8.0 mm per m² subject to the specific land use. Since this variable has a relatively low impact on the dynamics of runoff lines (Maniak 1997), the maximum depression storage is set to a lump value and is not differentiated according to the land use. As the depression storage is only important in rather lowly-elevated locations, the maximum depression storage is weighted using the slope of the specific area. As, according to Maniak (1997), the maximum depression storage decreases by 50% from 4-6 % slope, the volume of the depression storage halved for areas exceeding this slope. If the maximum depression storage is exceed on an area, spare water is released as surface runoff.

The middle pore storage

The water stored in the middle pores of the soil is held against gravity due to the adsorption powers. This means an active soil water potential is required in order to extract water from the middle pore storage. The potential for such a soil water suction is made available by evaporation. Two different cases have to be distinguished: the direct evaporation from the soil surface and the evaporation caused by transpiration of the vegetation cover. The direct evaporation of the soil surface is comparably low since only a few millimeters of dry soil can cause an effective isolation of the underlying layers regarding the evaporation. This isolation is shorted out by the roots of the vegetation cover, which makes a consistent exhaustion of water stored in the middle pores possible by transpiration. With increasing dehydration of the soil the actual evaporation decreases significantly in relation to potential evaporation. For simulating this reduction an established linear approach ([Gurtz et al. 1997]; [Schulla 1997]; [Uhlenbrook 1999]) is used or a nonlinear approach which has been developed for the model is applied.

When using the linear approach it is assumed that the real evaporation equals potential evaporation until a specific water saturation is achieved. When the value goes below this water saturation, the real evaporation decreases consistently in relation to potential evaporation until it is zero when reaching the permanent welting point (= complete emptying of nFk). As threshold value (soilLinRed) for this specific water saturation values between 0.8 to 0.6 are mentioned in the literature ([Gurtz et al. 1997]; [Menzel 1997]). This threshold value and the actual water saturation of the middle pore storage M (satMPS) is used to calculate a reduction factor (RF):

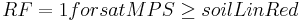
$RF = 1 for satMPS \geq soilLinRed$

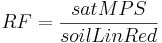
$RF = \frac{satMPS}{soilLinRed}$

The large pore storage

The water which is in the large pore storage (GPS) is subject to gravitation and is therefore considered as the source of actual flow processes and runoff generation of the soil in J2000. Filling the storage is done by the infiltration amount which remains after subtracting the inflow to the middle pore storage.

The different runoff behavior of different soils is reflected very well by the pore volumes which have been defined beforehand. Clayey soil has a relatively high proportion of fine and middle pores, whereas sandy soil has a comparably high amount of large pores. The generation of lateral and vertical runoff and the amount of precipitation is correspondingly different. The water which is stored in rather clayey soil contributes less to lateral and vertical runoff, under the same conditions (e.g. vegetation cover, slope etc.), than does rather sandy soil. In contrast, the water amount available for evaporation is significantly higher in clayey soils than in sandy soils. Clayey or silty soil, which lies between the above-mentioned soils according to their pore size, has the best water storage capacities since it has the highest amount of middle pores.

The water amount which generates runoff from the large pore storage in the time step is subject to the relative water saturation of the entire soil (LPS_soil) and is calculated according to:

$Q_{LPS} = (Sat_{soil})^\alpha\ \cdot LPS_{act} \,\,\, [mm]$

with:

Q_LPS: Outflow from LPS [mm]

Sat_soil: Relative water saturation of the soil at location [-]

α : calibration coefficient [-]

The advantage of this non-linear outfall function is that much less water runs off in low areal humidity than if it were a linear drain function. The common behavior of catchment areas which generate much more and faster runoff when there is high soil moisture (Baumgartner & Liebscher 1990; Dyck & Peschke 1995) than when there is low soil moisture (assuming the same precipitation amount) can be better displayed using an outfall function.

The gravitation water flowing out from the LPS (Q_LPS ) is distributed among three different target storage. A certain amount goes to the middle pores and is stored there for a longer period of time, a second part percolates into the groundwater storage (vertical component) and the remaining amount provides the source for interflow (lateral component). The size of the components is subject to soil-physical parameters (especially kf values) and the slope of the corresponding HRU. Therefore, it is assumed in the model that the slope area generates much interflow, whereas in almost evenly situated locations the percolation into the groundwater is the main component. The amount which goes from large pores into middle pores is, however, subject to the saturation of the middle pore storage. In order to determine of runoff amounts the slope and two kf values have to be specified for each HRU: The kf value of the soil horizon with the lowest permeability and the kf value of the overlying horizon.

Percolation and interflow generation

A certain amount of available gravitation water seeps through the entire soil and contributes to groundwater recharge. In the model presentation of the J2000 this percolated amount is represented as dependent on the slope of the corresponding HRU. The slope influences the percolation in that inclined areas have a higher amount of gravitation water as lateral runoff from unsaturated zones, i.e. the groundwater recharge is less in these areas than in evenly situated locations. The influence of the slope is taken into account with a gradient according to the following equation:

$grad_{perc} = (1 - tan \alpha)^\beta\ \,\,\, [-]$

α: slope of the corresponding HRU [degree]

β : shape parameter, calibration coefficient [-]

Using this equation the relation between vertical and lateral runoff is determined which can be adapted to the conditions in the catchment area with help of the calibration coefficient β. In addition, with this calibration coefficient the slope resulting from coarse-grained models which is systematically too low can be enhanced.

The water amount which is available for percolation is calculated according to:

$Perc_{pot}= grad_{perc} \cdot Q_{LPS} \,\,\, [mm]$

This percolation rate is then set against the calibration coefficient soilMaxPerc which describes the maximum percolation rate per time step.

And for the interflow Interflow(RD2):

$Interflow = 1- grad_{perc} \cdot Q_{LPS} \,\,\, [mm]$

Runoff detention

Both runoff components, direct runoff (RD1) and interflow (RD2) are delayed in time in order to take into account the areal expansion of the spatial model entity. The detention takes place using corresponding retention coefficients (soilConcRD1, soilConcRD2). The detention is calculated according to:

$RD1 = \frac{1}{soilConcRD1} \cdot RD1{gen} \,\,\, [mm]$

$RD2 = \frac{1}{soilConcRD2} \cdot RD2{gen} \,\,\, [mm]$

Nepal (2012) suggested that in the case of RD1, the delayed time may be different during high-flow periods due to non-linear behavior of a catchment. Beven (2001a) highlighted that the non-linear responses primarily exist due to two causes. The first reason is the antecedent condition when the relationship between rainfall and runoff is generally considered to be nonlinear because the wetter the catchment prior to a unit input of rainfall, the greater the runoff that will be generated. Second, a non-linearity exists also due to change of velocity with discharge. Average flow velocities increase with the flow with both surface and subsurface flow processes. Faster flow velocities mean that the runoff will reach a measurement point in the stream-channel flow system more quickly. In case of high precipitation events (such as during the monsoon season in the study area) which are responsible for high flood peaks, a high degree of non-linearity is noted. During those events, the soil becomes saturated by the initial rainfall events and a higher rainfall-runoff coefficient is likely after some periods of rainfall. These typical conditions have been taken into account by introducing a new parameter into the J2000 modelling system. The new parameter (concRD1Flood) is used by the model when the RD1_gen crosses a threshold value (RD1FloodThreshold) provided by a user. The value of (concRD1Flood) should be lower than concRD1 because it produces higher RD1 output flow.

$RD1_{flood} = \frac{1}{soilConcRD1Flood} \cdot RD1{gen} \,\,\, [mm]$

Diffusion

At the end of the time step a deficit of the middle pore storage (MPS) resulting from evaporation be balanced out by water from the large pore storage (LPS). This diffusion ( diff) is carried out using the calibration coefficient soilDiffMPSLPS according to:

$diff = actLPS \cdot (1-e\frac{-1\cdot diff }{satMPS}) \,\,\, [mm]$

For more information see also: [Baumgartner & Liebscher 1990], [Dyck & Peschke 1995], [Gurtz et al. 1997], [Maniak 1997], [Menzel 1997], [Scheffer & Schachtschabel 1984], [Schulla 1997], [Uhlenbrook 1999], [Wessolek 1993]

Groundwater module

The model structure of the groundwater module in J2000 allows the presentation of the groundwater runoff of all geological formations existing in the catchment area by considering their storage and runoff behavior. Those formations have to be parameterized separately. The geological units are subdivided into the upper groundwater storage (RG1) in the weathered loose material with high permeability and short retention time and the lower groundwater storage (RG2) in the matrix and in fissures and ravines of the bedrock with low permeability and long retention time. Correspondingly, two basic runoff components are generated, a fast one from the upper groundwater storage and a slow one from the lower groundwater storage. Filling the groundwater storage results from the vertical runoff component of the soil module (percolation), emptying can be done by the lateral underground runoff components and the capillary rise on the unsaturated zone. The parameterization of the groundwater storage is carried out using the maximum storage capacity of the upper (maxRG1) and the lower groundwater storage (maxRG2) as well as the retention coefficient for both storages, (kRG1) and (kRG2). The maximum storage capacity can be estimated by multiplying the part of the underground chamber with the thickness of the individual storages per m² standard area. Both parameters have to be defined for every geological unit separately and have to be saved in the corresponding parameter file. The following table shows an example of such a parameter file.

The first process to be calculated is the capillary rise. It is assumed that this action takes place in the slow groundwater storage RG2. The calculation is done using the actual storage amount actRG2, the humidity deficit (deltaSoilStor) or the relative saturation (satSoilStor) in the upper soil and the calibration parameter gwCapRise. Capillary rise is calculated if the current storage amount of the groundwater storage is higher than the soil humidity deficit and the calibration parameter gwCapRise is above zero. By putting it to zero the capillary rise can be prevented.

If capillary rise is calculated, first the rise rate inSoilStor is calculated:

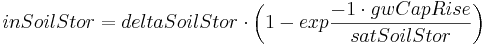
$inSoilStor = deltaSoilStor \cdot \left(1 - exp\frac{-1 \cdot gwCapRise}{satSoilStor} \right)$

It is then extracted from the groundwater storage RG2 and added to the upper soil water storage. After calculating the capillary rise the lateral inflow is considered. Hence, both inflow components inRG1 and inRG2 are added to the corresponding storages actRG1 and actRG2. If the maximum storage capacity is exceeded, surplus water is directly given to the runoff component.

The allocation of the percolation from the upper soil is carried out according to the slope of the specific model entity and a calibration coefficient (gwRG1RG2dist) in the following steps. First, the influence of the slope is considered:

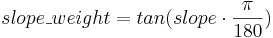
$slope\_weight = tan (slope \cdot \frac{\pi}{180} )$

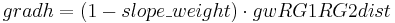
$gradh = (1 - slope\_weight) \cdot gwRG1RG2dist$

Then the percolation rate is allocated:

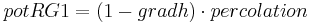
$potRG1 = (1-gradh) \cdot percolation$

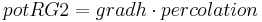
$potRG2 = gradh \cdot percolation$

The potential inflows are calibrated against the corresponding current storage. If RG2 cannot take the inflow pot_RG2 completely, the surplus is transferred to pot_RG1. If RG1 cannot take pot_RG1, the surplus is given to gwExcess. According to the model’s concept this variable can be assigned to a specific runoff component.

The calculation of water discharge is carried out according to the current storage amount in form of a linear storage-outflow function. The storage retention coefficients (kRG1, kRG2), which are considered as the time water rests in the specific storage, are a factor of the current storage volume (actRG1 and actRG2) used for the calculation of the groundwater outflow (outRG1 and outRG2) as follows:

$outRG1 = \frac{1}{gwRG1Fact \cdot kRG1} \cdot actRG1 \,\,\,[mm]$

$outRG2 = \frac{1}{gwRG2Fact \cdot kRG2} \cdot actRG2 \,\,\,[mm]$

The groundwater dynamics can be calibrated using parameters gwRG1Fact and gwRG2Fact.

Routing module

The J2000 module has two different routing components. The lateral routing component serves to simulate lateral flow processes in the catchment area until the water finally reaches a preflooder segment or a reservoir. In order to do so, the individual runoff components which are generated in the model entities are transferred to the corresponding recipient. This component does not have any calibration parameters.

The reach routing component is used for modeling flow processes in the on-site preflooder network of the catchment area. First, separate reaches have to be parameterized. The individual parameters which have to be assigned, are length in meters, slope in %, the mean width in meters and the reach roughness according to Manning-Strickler. Those are stored in a parameter file which is read by the model and by which the corresponding objects are generated. Additionally, the file contains information on the structure of the flow topology by noting the ID for every reach into which it empties. The reach representing the catchment outlet has to contain the ID 0.

The individual reaches receive water by neighboring spatial model entities and upstream reaches. In the reach, a velocity for water amount is calculated and then a certain amount is given to the next downstream reach based on the velocity and the length of the on-site preflooder. For the calculation a rectangular cross section is assumed to simplify matters. Although the complete amount of water is routed, the relative amounts of the individual runoff components are maintained, so they can be considered separately anytime and in every reach.

The module describes flow processes in the channel by using the kinematic wave approach and the calculation of velocity according to MANNING & STRICKLER. The only parameter that has to be set by the user (TA)(also referred as flowRouteTA) is a routing coefficient. It represents the runtime of the runoff wave which moves in the channel until it reaches the catchment outlet after a precipitation event. Its value is required for the calculation of the restraint coefficient (Rk) together with velocity of the river (v) and flow length (fl):

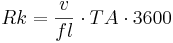
$Rk = \frac{v}{fl} \cdot TA \cdot 3600$

Before doing so, the velocity (v_new) has to be determined using the roughness factor by Manning (M), slope of the river bed (l) and the hydraulic radius (Rh). The hydraulic radius is calculated using the drained cross section (A) of the reach which results from the flow rate (q), velocity (v) and river bed width (b). For this approach, a start velocity (v_init) is assumed which is then iteratively adjusted with regard to the new calculated velocity (v_new) until both velocities differ in a value smaller than 0,001 m s^{-1}:

$Rh = \frac{A}{b + 2 \frac{A}{B}} \,\,\,\,[m]$

with: $A = \frac{q}{v_{init}} \,\,\,\,[m^2]$

$v_{new} = M \cdot Rh^{\frac{2}{3}} \cdot l^{\frac{1}{3}} \,\,\,\,[m^3/sec]$

$q = q_{act} \cdot e^{\frac{-1}{Rk}} \,\,\,\,[m^3/sec]$

Finally, the amount of water of the corresponding reach ( ) is calculated which goes to the runoff ( ) using the runoff restraint coefficient ( ) which has been generated.

$q = q_{act} \cdot e^{\frac{-1}{Rk}} \,\,\,\,[m^3/sec]$

The higher the assumed value of TA, the faster does the runoff wave move within a certain time span and the less water remains in the channel.

J2000 modules in detail

Contents

Precipitation distribution module

Interception module

Snow module

Glacier module

Soil water module

Groundwater module

Routing module

Views

Personal tools

Navigation

Search

Toolbox

In other languages