Gaussian Process Regression

Contents 1 Abstract 2 Download 3 Quick start 4 Manual 4.1 data file 4.2 input dimension 4.3 relevant timesteps 4.4 gaps 4.5 enable crossvalidation 4.6 enable splitvalidation 4.7 reduced training size 5 covariance function 5.1 mean function 5.2 do optimization 5.3 result file 6 Literature

Abstract

During the last decade the number of publications on the field of kernel machines has increased enormously. Widely known are studies on Support Vector Machines (SVM), much activity was also spent on applying Gaussian processes to problems on the area of machine learning. This method represents a universal and practical approach to learning with kernel machines. Because of its solid statistical foundation learning with Gaussian processes has advantages over other empirical approaches concerning interpretability of model predictions. It also offers an established framework for model selection and subsequent model setup.

Because of ongoing theoretical and practical developments during the last years, Gaussian processes are nowadays considered as a serious alternative in the area of supervised learning. Because of their promising characteristics these methods are especially suited for Rainfall-Runoff-Modelling. Nevertheless, so far they have not attracted much interest in this domain.

The Gaussian process regression is based on the assumption that observations follow a normally distributed stochastic process. This leads to the conclusion, that new observations do not change the probability distribution of earlier ones. Based on this simple property Gaussian process regression allows predictions for unknown values. This paper describes an application of a Gaussian process regression based simulation model on the River Ouse dataset. The results show that this model is very well suited for an automated short-term runoff prediction which is only based on measured precipitation and runoff.

Download

zip
Poster

Quick start

You need to have JAVA Runtime Environment (JRE) installed on your machine. It can be downloaded for free here

• Now download JAMS Prediction Package from this site.
  
• Extract the compressed zip file.
  
• Run JAMS.exe
  
• From the menu, choose File -> Load Model Configuration
  
• From the installation directory, select the predict.jam model configuration file
  
• Apply settings to initial model parameters as you like
  
• Run the model and enjoy ;)
  
• To see information about current model execution, choose Logs->Model Info Log
  
• The predictions will be saved in a file named result.txt
  

Manual

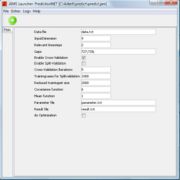
After starting JAMS you will see a window like the one in figure 1.

There are some model attributes and parameters which can be changed.

data file

The data file is a simple text file. It contains all time series, which should be used for training, validation and verification. The datafile has a table like structure. Each row consists of all relevant measurements at time t, which are represented as tab seperated floating point numbers. It is important that every row has the same number of elements. The value, which is supposed to be predicted, must be the last element in each row. In cases in which this value is unknown, simply write an arbitary number in that column, but remember that you should not use them in the training process. A simple data file will look like that:

 1.0 0.0 0.5 11.1 -0.1
 0.0 0.2 0.3 11.0 -0.5
 2.3 3.1 1.0 10.5  1.0
 5.0 6.1 4.2 11.5  2.1
 3.0 5.2 1.0 13.6  0.0
 0.8 1.1 0.5 13.6 -0.7

input dimension

Specifies the number of columns -1 in the data file. (e.g 4 in the above case)

relevant timesteps

Number of timesteps, which should be used for each prediction. That means if you use a relevant time k = 1, than the prediction is based only on the current time step t. With a relevant time of k = 2, timestep t and t-1 will be used.

gaps

If there are gaps in the datafile, than you should add the row before and after the gap here. Each value must be seperated by a ";" Here is an example of a file with one gap between line 3 and 4

  1.1.2007  1.0 0.0 0.5 11.1 -0.1
  2.1.2007  0.0 0.2 0.3 11.0 -0.5
  3.1.2007  2.3 3.1 1.0 10.5  1.0
  6.1.2007  5.0 6.1 4.2 11.5  2.1
  7.1.2007  3.0 5.2 1.0 13.6  0.0
  8.1.2007  0.8 1.1 0.5 13.6 -0.7

Gaps should look like that:

  3;4

enable crossvalidation

If you check this box, a crossvalidation is performed. You can specify the number of crossvalidation iterations in the textfield below.

enable splitvalidation

If you check this box, a splitvalidation is performed. You can specify the number of datasets which are used for training in the textfield below. The remaining datasets are used for validation.
NOTICE: you shouldn´t enable both boxes at the same time.

reduced training size

If you have a large number of datasets, training will be computationally extremly expensive. It is also possible, that you will be running out of memory. That is why you can reduce the number of datasets used for training. The procedure which is used for this reduction tries to select datasets which are as different as possible. If you do not want to reduce your number of datasets, simply choose a number which is larger than the amount of datasets you have.

covariance function

Covariance Function which is used for regression. The following values are possible:

• Squared Exponential: 2
• Matérn Class Function: 3
• Rational quadratic: 5
• Neural Network covariance function: 6
• Extended Neural Network covariance function: 8

mean function

A value of one indicates, that a linear regression is applied simulatiously. In many extrapolation cases this will increase prediction performance. A value of zero, skips that part.

do optimization

Every covariance function has a number of parameters, which have to be determined. If you check this box, a gradient descent optimization technique is executed, which tries to find an optimal set of parameters, which are stored afterwards in a parameter file. If you don´t want to optimize, than the algorithm tries at first to read the parameter file. If this file does not exist than standardparameters are used, which are not optimal.

result file

name of file in which the results are saved.

Literature

• Rasmussen,C. and C. Williams: Gaussian Processes for Machine Learning; The MIT Press, 2006. ISBN 0-262-18253-X
• Scholkopf, B. and A. Smola: Learning with Kernels: Support Vector Machines, Regularization, Optimization and Beyond. MIT Press Cambridge, MA, USA, 2001
• Stein, M. Interpolation of Spatial Data: Some Theory for Kriging. Springer, 1999.
• Blight, B. and L. Ott.: A Bayesian approach to model inadequacy for polynomial regression. Biometrika, 62(1):79, 1975.
• Berger, J. O. S: Statistical Decision Theory and Bayesian Analysis. Spring, New York. 1985